GAN – Perché è così difficile addestrare le reti avversarie generative!

È più facile riconoscere un quadro di Monet che disegnarlo. I modelli generativi (creazione di dati) sono considerati molto più difficili rispetto ai modelli discriminativi (elaborazione di dati). Anche l’addestramento di GAN è difficile. Questo articolo fa parte della serie GAN e indagherà sul perché l’addestramento sia così sfuggente. Attraverso lo studio, comprendiamo alcuni problemi fondamentali che guidano le direzioni di molti ricercatori. Esamineremo alcune divergenze in modo da sapere dove la ricerca può dirigersi. Prima di esaminare i problemi, facciamo un rapido riepilogo di alcune equazioni GAN. Se siete poco pratici di questo argomento, invece, ve ne parla meglio Valerio Massoli nel nostro corso di Modelli Generativi.
GAN
La GAN campiona il rumore z utilizzando una distribuzione normale o uniforme e utilizza un generatore di rete profonda G per creare un’immagine x (x=G(z)).
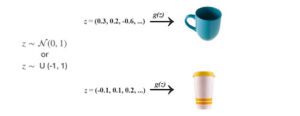
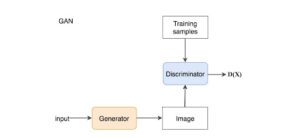
In GAN, aggiungiamo un discriminatore per distinguere se l’input del discriminatore è reale o generato. Il discriminatore emette un valore D(x) per stimare la probabilità che l’input sia reale.
Funzione obiettivo e gradienti
Il GAN è definito come un gioco di minimax con la seguente funzione obiettivo.
![]()
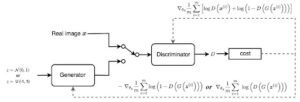
Il diagramma seguente riassume il modo in cui addestriamo il discriminatore e il generatore utilizzando il gradiente corrispondente.
Problemi GAN
Molti modelli GAN presentano i seguenti problemi principali:
– Non convergenza: i parametri del modello oscillano, si destabilizzano e non convergono mai,
– Collasso del modo: il generatore collassa e produce una varietà limitata di campioni,
– Diminuzione del gradiente: il discriminatore ottiene un successo eccessivo che fa svanire il gradiente del generatore e non impara nulla,
– Sbilanciamento tra il generatore e il discriminatore che causa overfitting, &
– Elevata sensibilità alle selezioni degli iperparametri.
Modalità
Le distribuzioni dei dati reali sono multimodali. Ad esempio, in MNIST esistono 10 modalità principali, dalla cifra “0” alla cifra “9”. I campioni sottostanti sono stati generati da due GAN diversi. La riga superiore produce tutte le 10 modalità, mentre la seconda riga crea una sola modalità (la cifra “6”). Questo problema è chiamato mode collapse quando vengono generate solo poche modalità di dati.

Equilibrio di Nash
Il GAN si basa sul gioco non cooperativo a somma zero. In breve, se uno vince l’altro perde. Un gioco a somma zero è anche chiamato minimax. Il vostro avversario vuole massimizzare le sue azioni e le vostre azioni devono minimizzarle. Nella teoria dei giochi, il modello GAN converge quando il discriminatore e il generatore raggiungono un equilibrio di Nash. Questo è il punto ottimale per l’equazione minimax che segue.
![]()
Poiché entrambe le parti vogliono indebolire gli altri, si ha un equilibrio di Nash quando uno dei due giocatori non cambia la propria azione indipendentemente da ciò che può fare l’avversario. Si considerino due giocatori A e B che controllano rispettivamente il valore di x e y. Il giocatore A vuole massimizzare il valore xy, mentre B vuole minimizzarlo.
![]()
L’equilibrio di Nash è x=y=0. Questo è l’unico stato in cui l’azione dell’avversario non ha importanza. È l’unico stato in cui le azioni dell’avversario non cambiano l’esito della partita.
Vediamo se possiamo trovare facilmente l’equilibrio di Nash usando la discesa del gradiente. Aggiorniamo i parametri x e y in base al gradiente della funzione valore V.
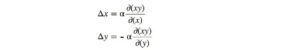
dove α è il tasso di apprendimento. Quando tracciamo i valori di x, y e xy rispetto alle iterazioni di addestramento, ci rendiamo conto che la nostra soluzione non converge.
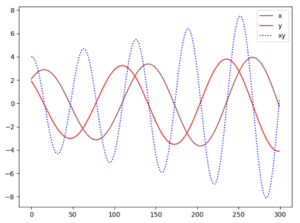
Se aumentiamo il tasso di apprendimento o addestriamo il modello più a lungo, possiamo vedere che i parametri x, y sono instabili con grandi oscillazioni.
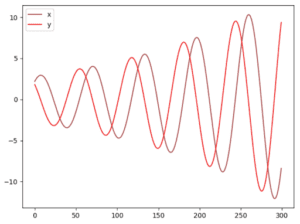
Il nostro esempio è un’ottima dimostrazione del fatto che alcune funzioni di costo non convergeranno con la discesa del gradiente, in particolare per un gioco non convesso. Questo problema può essere visto anche in modo intuitivo: l’avversario prende sempre le contromisure alle sue azioni, il che rende più difficile la convergenza dei modelli.
Le funzioni di costo potrebbero non convergere utilizzando la discesa del gradiente in un gioco minimax.
Modello generativo con KL-Divergence
Per comprendere il problema della convergenza nel GAN, studieremo innanzitutto la divergenza KL e la divergenza JS. Prima della GAN, molti modelli generativi creano un modello θ che massimizza la stima di massima verosimiglianza (Maximum Likelihood Estimation MLE), ossia trovano i migliori parametri del modello che si adattano maggiormente ai dati di addestramento.
![]()
Ciò equivale a minimizzare la divergenza KL(p,q) (prova) che misura come la distribuzione di probabilità q (distribuzione stimata) diverge dalla distribuzione di probabilità attesa p (distribuzione reale).
![]()
La divergenza KL non è simmetrica.
![]()
KL(x) scende a 0 per l’area in cui p(x) → 0. Ad esempio, nella figura a destra qui sotto, la curva rossa corrisponde a D(p, q). Essa scende a zero quando x>2 dove p si avvicina a 0.
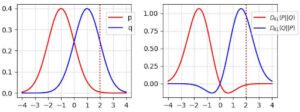
Qual è l’implicazione? La divergenza KL DL(p, q) penalizza il generatore se manca alcune modalità di immagini: la penalità è alta quando p(x) > 0 ma q(x) → 0. Tuttavia, è accettabile che alcune immagini non sembrino reali. La penalità è bassa quando p(x) → 0 ma q(x)>0. (Qualità inferiore ma campioni più diversificati)
D’altra parte, la divergenza KL inversa DL(q, p) penalizza il generatore se le immagini non sembrano reali: la penalità è alta se p(x) → 0 ma q(x) > 0. Ma esplora una minore varietà: la penalità è bassa se q(x) → 0 ma p(x) > 0. (Qualità migliore ma campioni meno diversificati)
Alcuni modelli generativi (diversi dai GAN) utilizzano il MLE (alias KL-divergence) per creare modelli. Inizialmente si riteneva che la divergenza KL causasse una qualità inferiore delle immagini (immagini sfocate). Ma è bene sapere che alcuni esperimenti empirici hanno smentito questa affermazione.
Divergenza JS
La divergenza JS è definita come:
![]()
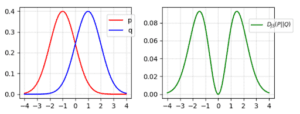
La divergenza JS è simmetrica. A differenza della divergenza KL, penalizzerà fortemente le immagini scadenti. (quando p(x)→ 0 e q(x) > 0) Nella GAN, se il discriminatore è ottimale (con buone prestazioni nel distinguere le immagini), la funzione obiettivo del generatore diventa (prova):
![]()
Quindi, l’ottimizzazione del modello generativo viene trattata come l’ottimizzazione della divergenza JS. Negli esperimenti, GAN produce immagini più belle rispetto ad altri modelli generativi che utilizzano la divergenza KL. Seguendo la logica dell’ultima sezione, le prime ricerche ipotizzano che l’ottimizzazione della JS-divergenza, piuttosto che della KL-divergenza, crei immagini migliori ma meno diversificate. Tuttavia, alcuni ricercatori hanno poi ritrattato queste affermazioni perché gli esperimenti con la GAN che utilizza MLE producono immagini di qualità simile, ma soffrono ancora del problema della diversità delle immagini. Tuttavia, sono già stati compiuti sforzi significativi per studiare la debolezza della JS-Divergence nell’addestramento della GAN. Questi lavori sono significativi a prescindere dai dibattiti. Pertanto, in seguito approfondiremo i problemi della JS-divergence.
Gradienti che svaniscono nella JS-Divergence
Ricordiamo che quando il discriminatore è ottimale, la funzione obiettivo del generatore è:
![]()
Cosa succede al gradiente di divergenza JS quando la distribuzione dei dati q delle immagini del generatore non corrisponde alla verità di base p delle immagini reali. Consideriamo un esempio in cui p e q sono distribuiti in modo gaussiano e la media di p è zero. Consideriamo q con medie diverse per studiare il gradiente di JS(p, q).
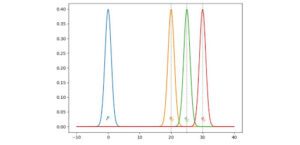
In questo caso, tracciamo la divergenza JS(p, q) tra p e q con medie di q che vanno da 0 a 30. Come mostrato di seguito, il gradiente della divergenza JS svanisce da q1 a q3. Il generatore GAN apprenderà con estrema lentezza quando il costo è saturo in queste regioni. In particolare, all’inizio dell’addestramento, p e q sono molto diversi e il generatore apprende molto lentamente.
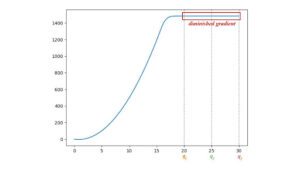
Gradienti instabili
A causa della scomparsa del gradiente, il documento originale della GAN propone una funzione di costo alternativa per risolvere il problema della scomparsa del gradiente.
![]()
Il gradiente corrispondente, secondo un’altra ricerca di Arjovsky, è il seguente:
![]()
Include un termine di divergenza KL inversa che Arjovsky utilizza per spiegare perché la GAN ha un’immagine di qualità superiore ma meno diversificata rispetto ai modelli generativi basati sulla divergenza KL. Ma la stessa analisi sostiene che i gradienti fluttuano e causano instabilità al modello. Per illustrare il punto, Arjovsky congela il generatore e addestra il discriminatore in modo continuo. Il gradiente del generatore inizia ad aumentare con le varianti più grandi.
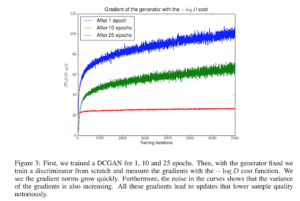
L’esperimento di cui sopra non è il modo in cui addestriamo le GAN. Tuttavia, dal punto di vista matematico, Arjovsky dimostra che la funzione obiettivo del primo generatore GAN ha gradienti che svaniscono e la funzione di costo alternativa ha gradienti fluttuanti che causano l’instabilità dei modelli. Dopo l’articolo originale sulla GAN, c’è stata una corsa all’oro per trovare nuove funzioni di costo, come LSGAN, WGAN, WGAN-GP, BEGAN ecc… Alcuni metodi si basano su nuovi modelli matematici e altri su intuizioni supportate da esperimenti. L’obiettivo è trovare una funzione di costo con gradienti più morbidi e non variabili.
Tuttavia, un documento di Google Brain del 2017, “Are GANs Created Equal?”, sostiene che
Infine, non abbiamo trovato prove che dimostrino che uno degli algoritmi testati superi costantemente quello originale.
Se le nuove funzioni di costo proposte dovessero dare il colpo di grazia nel migliorare la qualità dell’immagine, non ci sarà più questo dibattito. Anche l’immagine apocalittica delle funzioni di costo originali, ricavata dal modello matematico di Arjovsky, non si concretizza del tutto. Ma voglio mettere in guardia i lettori dal dichiarare prematuramente che le funzioni di costo non sono importanti. Le mie riflessioni sul documento di Google Brain sono disponibili qui. Qual è la mia opinione? L’addestramento della GAN fallisce facilmente. Invece di provare molte funzioni di costo all’inizio, eseguite prima il debug del progetto e del codice. Poi cercate di mettere a punto gli iperparametri, perché i modelli GAN sono sensibili ad essi. Fatelo prima di provare funzioni di costo a caso.
Perché il mode collapse in GAN?
Il collasso di modalità è uno dei problemi più difficili da risolvere in GAN. Un collasso completo non è comune, ma un collasso parziale si verifica spesso. Le immagini sottostanti con lo stesso colore sottolineato si assomigliano e la modalità inizia a collassare.

Vediamo come può avvenire. L’obiettivo del generatore GAN è quello di creare immagini che possano ingannare il discriminatore D il più possibile.
![]()
Ma consideriamo un caso estremo in cui G viene addestrato in modo estensivo senza aggiornamenti a D. Le immagini generate convergeranno per trovare l’immagine ottimale x* che inganna maggiormente D, l’immagine più realistica dal punto di vista del discriminatore. In questo caso estremo, x* sarà indipendente da z.
![]()
Questa è una cattiva notizia. La modalità collassa in un singolo punto. Il gradiente associato a z si avvicina a zero.
![]()
Quando si riavvia l’addestramento nel discriminatore, il modo più efficace per rilevare le immagini generate è quello di rilevare questa singola modalità. Poiché il generatore desensibilizza già l’impatto di z, il gradiente del discriminatore spingerà probabilmente il singolo punto verso la modalità successiva più vulnerabile. Non è difficile da trovare. Il generatore produce un tale sbilanciamento delle modalità in fase di addestramento da deteriorare la sua capacità di rilevarne altre. Ora, entrambe le reti sono sovra-adattate per sfruttare le debolezze a breve termine dell’avversario. Questo si trasforma in un gioco del gatto e del topo e il modello non converge.
Nel diagramma sottostante, la GAN Unroll riesce a produrre tutte le 8 modalità di dati previste. La seconda riga mostra un’altra GAN in cui la modalità collassa e ruota verso un’altra modalità quando il discriminatore la raggiunge.

Durante l’addestramento, il discriminatore viene costantemente aggiornato per individuare gli avversari. Pertanto, è meno probabile che il generatore sia sovraadattato. In pratica, la nostra comprensione del mode collapse è ancora limitata. La nostra spiegazione intuitiva di cui sopra è probabilmente eccessivamente semplificata. I metodi di mitigazione vengono sviluppati e verificati con esperimenti empirici. Tuttavia, l’addestramento di GAN è ancora un processo euristico. Il collasso parziale è ancora comune.
Ma il collasso di modalità non è solo una cattiva notizia. Nel trasferimento di stile tramite GAN, siamo felici di convertire un’immagine solo in una buona immagine, piuttosto che trovare tutte le varianti. In effetti, la specializzazione nel collasso parziale della modalità a volte crea immagini di qualità superiore.
Ma il collasso di modalità rimane uno dei problemi più importanti da risolvere per GAN.
Stima implicita della massima verosimiglianza (IMLE)
(Crediti: i diagrammi di questa sezione sono stati ricavati o modificati dalla presentazione IMLE).
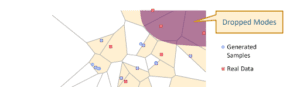
Dopo la stesura di questo articolo, è stato pubblicato un nuovo documento di ricerca che spiega e risolve il problema del collasso delle modalità. Consideriamo i quadrati rossi qui sotto come i dati reali e quelli blu come i campioni generati.

Il discriminatore GAN crea regioni in giallo per distinguere i dati reali da quelli generati.
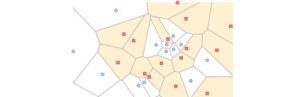
Nel processo di addestramento, il generatore genera dati per spostare i campioni generati verso il confine decisionale, mentre il discriminatore restringe ulteriormente il confine.

Ma il generatore non ha alcuna garanzia di generare campioni che coprano tutte le modalità del processo. Come mostrato nell’esempio, alcune modalità possono essere tralasciate nel processo e non possono essere recuperate.
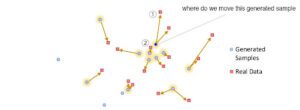
IMLE inverte il meccanismo. In GAN, spostiamo i campioni generati verso il confine più vicino. Ad esempio, spostiamo il punto blu in basso verso ②. Ma in IMLE, per ogni dato reale, chiediamo qual è il campione generato più vicino. Quindi addestriamo il modello a spostare il punto blu verso ①.
IMLE non è un modello GAN. Pertanto, non lo elaboreremo ulteriormente in questa sede.
Iperparametri e formazione
Nessuna funzione di costo funziona senza buoni iperparametri e la loro messa a punto richiede tempo e molta pazienza. Nuove funzioni di costo possono introdurre iperparametri che hanno prestazioni sensibili.
La messa a punto degli iperparametri richiede pazienza. Nessuna funzione di costo funzionerà senza dedicare tempo alla messa a punto degli iperparametri.
Equilibrio tra discriminatore e generatore
La mancata convergenza e il collasso dei modi sono spesso spiegati come uno squilibrio tra il discriminatore e il generatore. La soluzione più ovvia è quella di bilanciare il loro addestramento per evitare l’overfitting. Tuttavia, sono stati fatti pochissimi progressi, ma non per la mancanza di tentativi. Alcuni ricercatori ritengono che questo non sia un obiettivo fattibile o auspicabile, poiché un buon discriminatore fornisce un buon feedback. L’attenzione si è quindi spostata su funzioni di costo con gradienti non variabili.
Costo e qualità dell’immagine
In un modello discriminativo, la perdita misura l’accuratezza della previsione e viene utilizzata per monitorare i progressi dell’addestramento. Tuttavia, la perdita nella GAN misura quanto stiamo facendo bene rispetto al nostro avversario. Spesso il costo del generatore aumenta, ma la qualità dell’immagine migliora. Si torna a esaminare manualmente le immagini generate per verificare i progressi. Ciò rende più difficile il confronto tra i modelli, con conseguenti difficoltà nella scelta del modello migliore in un’unica esecuzione. Complica inoltre il processo di messa a punto.
Articolo originale di Jonathan Hui
Share:


