L’equazione di Schrödinger: Spiegata
L'equazione più importante della meccanica quantistica
I fondamenti della meccanica quantistica sono spesso inaccessibili alla grande maggioranza. Insieme alla controintuizione della fisica quantistica, c’è un mondo di pregiudizi. Convenzionalmente si ritiene che sia particolarmente difficile. Naturalmente, non è come sembra. Questo è il mio tentativo di spiegare l’equazione di Schrödinger ai non addetti ai lavori. Un’equazione che ha innegabilmente cambiato il modo in cui percepiamo la realtà. Avete mai sentito parlare del gatto di Schrödinger? Ne parla anche Antonio Macaluso nel nostro corso di Quantum Computing da lui tenuto.

Citando Wikipedia:
L’equazione di Schrödinger è un’equazione differenziale parziale lineare che regola la funzione d’onda di un sistema quantomeccanico.
Anche se probabilmente non ha molto senso. Cosa significa dire che una funzione è lineare? O che è parzialmente differenziata? Rispondere a questa domanda significherebbe approfondire la matematica. Ma per quanto ci riguarda oggi:
L’equazione di Schrödinger fornisce un modo per calcolare la funzione d’onda di un sistema e il modo in cui essa cambia dinamicamente nel tempo.
Concettualmente, l’equazione di Schrödinger è la controparte quantistica della seconda legge di Newton nella meccanica classica. Data una serie di condizioni iniziali note, la seconda legge di Newton fa una previsione matematica sul percorso che un dato sistema fisico seguirà nel tempo. L’equazione di Schrödinger fornisce l’evoluzione di una funzione d’onda nel tempo.
Entra: L'equazione di Schrödinger
L’equazione può essere scritta in varie forme. Tuttavia, nella sua forma più semplice, si presenta come segue:
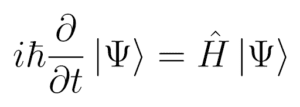
Medium non è molto pratico nell’inserire equazioni, quindi ecco un png al suo posto!
Questa equazione dall’aspetto scoraggiante è il punto in cui ci troviamo. Si tratta, da ogni punto di vista, del postulato di meccanica quantistica di maggior successo di tutti i tempi. Alla fine di questo articolo, avrete almeno una comprensione di base del significato di tutto questo.
Per prima cosa, iniziamo con la psi, la 23a lettera greca. Ψ (psi, pronunciato con la /ps/ di “lapse” seguita da una /eye/) rappresenta la funzione d’onda di un sistema quantistico. Ebbene Ψ, in particolare, ci dice quanto è probabile trovare una particolare particella in diverse regioni dello spazio nel nostro sistema.
Ora, le funzioni d’onda. Cosa sono? Ho dedicato una lettura di 7 minuti se volete saperne di più, ma in breve una funzione d’onda è una descrizione matematica di tutto ciò che sappiamo su un particolare sistema quantistico. Un sistema quantistico è ovviamente un “sistema” che studiamo utilizzando la meccanica quantistica. Può essere qualsiasi cosa. Mettiamo un elettrone in un campo elettrico e quello è un sistema. E se usiamo la meccanica quantistica per studiarlo, diventa un sistema quantistico.
Ψ² ∝ distribuzione di probabilità di trovare una particella in un determinato punto.
Il linguaggio della fisica quantistica
Un’introduzione a ket, funzioni d’onda e sistemi quantistici
medium.com
Ma non scriviamo semplicemente Ψ quando rappresentiamo un sistema quantistico. In realtà lo scriviamo in questo modo: |Ψ⟩. Una linea retta a sinistra e una parentesi angolare a destra. Ora, questa “cosa” si chiama ket. Si scrive così per una serie di ragioni matematiche. Ma ai fini di questo articolo, ciò che dobbiamo sapere è che il ket ci permette di capire che stiamo osservando un sistema quantistico. È solo una notazione di convenienza. Il ket è il simbolo meccanico quantistico che codifica lo stato di un sistema. Quindi, in sostanza, il ket, che è lo stato quantistico, ci dice lo stato del nostro sistema quantistico. Chi l’avrebbe mai detto?
|Ψ⟩ = stato del sistema quantistico
Ora che questo è stato stabilito, è possibile dedurre che gli altri elementi dell’equazione di Schrödinger influenzeranno lo stato quantistico in un modo o nell’altro. Ciò significa che quello che stiamo studiando è il comportamento dello stato quantistico.
Esaminiamo ora la prima parte:

Questa parte è relativamente semplice da capire. Innanzitutto, è importante sapere che sia i che hbar sono costanti. Cioè sono solo numeri. Numeri molto importanti, ma pur sempre numeri.
i, come si è visto, è la radice quadrata di 1 negativo. Se non avete familiarità con i numeri complessi, potreste pensare che questo non sia possibile. Ma è così. Non approfondiamo troppo il come. Prendetemi solo per fede cieca.
i = √(-1)
Veniamo allo strano ds:

Questo bit si pronuncia come “doh by doh t”. Questa notazione vi sarà familiare se avete studiato calcolo alle superiori. Ma se non l’avete fatto, significa semplicemente il cambiamento di qualcosa (in questo caso, il nostro stato quantistico) rispetto al tempo. Naturalmente, ci sono alcune complessità matematiche che ho tralasciato, ma l’essenza è che questo operatore differenziale misura la velocità con cui qualcosa cambia rispetto al tempo.
Quindi ora abbiamo questo:
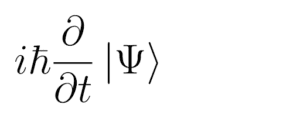
Se mettiamo tutto insieme, sappiamo che abbiamo un numero, i hbar, moltiplicato per il doh per doh t dello stato quantico. Il doh per doh t dello stato quantico misura il cambiamento dello stato quantico rispetto al tempo. Abbiamo coperto la maggior parte dell’equazione. Ma il bello deve ancora venire.
Il bello
Il lato destro dell’equazione: Ĥ|Ψ⟩.
Questo (l’Ĥ) è noto come operatore Hamiltoniano. La prima lettera di “Hamiltonian” spiega perché è indicata con una H, ma perché il cappello? Nella meccanica quantistica esistono degli operatori. Sono scritti con un piccolo cappello in cima. In pratica “operano” sugli stati quantistici. Fanno qualcosa allo stato quantico.
L’operatore hamiltoniano è il più grande degli operatori quantistici. È legato all’energia totale del sistema. Spiegato brevemente:
Ĥ = energia cinetica+ energia potenziale+ qualsiasi altra energia del sistema.
Quindi, in sostanza, tutto ciò che sta accadendo è che lo stato quantistico, |Ψ⟩, cambia rispetto al tempo in un modo molto specifico, a seconda dell’energia totale del sistema. Questa equazione, quindi, ci permette di prevedere il comportamento di un sistema quantistico se possiamo scrivere matematicamente tutte le energie del nostro sistema. Un gioco da ragazzi.
Tuttavia, come sempre, c’è un’avvertenza. Per sistemi più grandi di poche particelle, questo diventa impossibile molto rapidamente. In altre parole, è abbastanza facile trovare un sistema che non può essere risolto analiticamente con l’equazione di Schrödinger. Abbiamo bisogno di metodi numerici che vadano oltre. Anche gli esseri umani hanno i loro fallimenti, quindi i computer lo fanno per noi. Ma anche oggi i computer più potenti non sono in grado di analizzare sistemi quantistici più grandi di qualche decina di atomi.
L'atomo di elio
Per dimostrare la complessità dell’Hamiltoniana, mettiamola a confronto con un atomo relativamente semplice. L’atomo di elio. L’unico atomo più semplice di questo è l’atomo di idrogeno. Ora dobbiamo già fare alcune ipotesi. Innanzitutto, assumiamo che il nucleo dell’atomo rimanga fisso nello spazio. In altre parole, tutte le particelle del nucleo sono stazionarie. Anche se non è quasi mai così, il nucleo si muove un po’. Anche in questa situazione estremamente semplificata, l’hamiltoniana del nostro sistema ha un aspetto simile a questo:
![]()
L'hamiltoniana dell'atomo di elio!
Contiene i seguenti termini (in ordine di apparizione): l’energia cinetica del primo elettrone, l’energia cinetica del secondo elettrone, l’attrazione elettrostatica tra il nucleo e il primo elettrone, la stessa cosa con il secondo elettrone e la repulsione elettrostatica tra i due elettroni. Ricordiamo che questo modello è talmente semplificato che non tiene conto di tutto ciò che accade al sistema quantistico. Inoltre, non abbiamo considerato gli spin degli elettroni, gli spin dei protoni e molto altro.
Quindi, in un certo senso, anche se disponiamo di un’equazione straordinariamente potente, la matematica che vi sta dietro può richiedere molto tempo. Spero che abbiate imparato qualcosa sull’equazione di Schrödinger.
Articolo originale di Yash
https://medium.com/quantafy/the-most-important-equation-of-quantum-physics-33a630ce9a0d
Share:


