Predizione delle serie temporali attraverso il meccanismo dell’attenzione e il Deep Learning
Una panoramica dell’architettura e dei dettagli dell’implementazione di uno degli algoritmi più importanti di Deep Learning per la predizione di serie temporali
Articolo originale in lingua inglese di Marco del Pra

Motivazioni
La predizione delle serie temporali (in inglese Time Series Forecasting) è sempre stata un’area di ricerca molto importante in diversi campi perché molti tipi di dati vengono registrati come serie temporali. Ad esempio possiamo trovare moltissimi dati temporali in medicina, previsioni meteo, biologia, supply chain, previsione dei prezzi delle azioni ecc.
Data la disponibilità crescente di dati e di capacità computazionale negli ultimi anni, il Deep Learning è diventato parte fondamentale dei modelli di nuova generazione per la predizione di serie temporali, ottenendo risultati davvero eccellenti.
Mentre nei modelli di Machine Learning classici – come modelli autoregressivi (AR) o smoothing esponenziale – l’ingegnerizzazione delle caratteristiche (feature engineering) viene eseguita manualmente e spesso alcuni parametri sono ottimizzati considerando anche conoscenze del dominio, i modelli di Deep Learning apprendono caratteristiche e dinamiche solamente e direttamente dai dati. Grazie a questo il processo di preparazione dei dati viene velocizzato e i modelli sono in grado di imparare pattern più complessi all’interno dei dati in modo più completo.
Dato che diversi problemi di serie temporali sono studiati in molti campi diversi, negli ultimi anni è stato sviluppato un gran numero di nuove architetture. Ciò è stato semplificato anche dalla crescita di disponibilità di framework open source che rendono più facile e veloce lo sviluppo di nuove componenti personalizzate delle reti. In questo articolo riassumiamo gli approcci più comuni di Deep Learning rispetto alla previsione di serie temporali.
Applicazioni
Vediamo ora alcune applicazioni importanti della previsione di serie temporali
- Previsione dei prezzi delle azioni: per prevedere i prezzi delle azioni si utilizzano molti modelli avanzati di previsione di serie temporali, poiché nelle sequenze storiche c’è molto rumore e l’informazione contiene un alto livello di incertezza che può dipendere da svariati fattori, non sempre strettamente collegati col mercato azionario
- Previsioni del tempo: modelli di previsione delle serie temporali sono ampiamente utilizzati per migliorare l’accuratezza delle previsioni meteo
- Previsione del traffico: le applicazioni di pianificazione viaggi utilizzano modelli di previsione delle serie temporali per predire il traffico lungo la strada al fine di decidere con maggiore accuratezza il percorso più veloce per arrivare alla destinazione selezionata
- Turnover: molte aziende utilizzano modelli di previsione delle serie temporali per prevedere in quale mese ci si può aspettare un turnover più alto in modo da attuare i migliori piani di fidelizzazione dei dipendenti
- Generazione di testo: quando scriviamo qualcosa sullo smartphone vengono suggerite le lettere, o addirittura l’intera parola successiva considerando quali sono state le ultime parole e lettere digitate
Componenti delle serie temporali
Innanzitutto è importante spiegare quali sono le maggiori componenti delle serie temporali
- Tendenze a lungo termine: direzione generale dei dati, ottenuta ignoranti qualsiasi effetto a breve termine come variazioni stagionali o rumore
- Stagionalità: si riferisce alle fluttuazioni periodiche che si ripetono per tutto il periodo della serie temporale
- Stazionarietà: caratteristica importante delle serie temporali. Una serie temporale viene definita stazionaria se la sua media, varianza e covarianza non cambiano significativamente nel tempo. Ci sono diverse trasformazioni che possono estrarre la componente stazionare di un processo non-stazionario
- Rumore: ciascun set di dati contiene anche rumore, ovvero fluttuazioni randomiche o variazioni legate a fattori che non possono essere controllati
- Autocorrelazione: correlazione tra la serie temporale ed una versione ritardata di sé stessa. Viene utilizzata per identificare stagionalità e tendenze in una serie di dati temporali.
Previsione di serie temporali con il Machine Learning Tradizionale
Prima di parlare di metodi di Deep Learning per la previsione di serie temporali, è utile ricordare che i modelli di Machine learning più classici utilizzati per risolvere questo tipo di problemi sono i modelli ARMA e lo smoothing esponenziale.
Un modello ARMA si costruisce combinando due approcci: Autoregressivo (AR) e Media Mobile (Moving Average in inglese). E’ un modello molto semplice, ciononostante permette di ottenere buoni risultati. Include parametri che tengono conto di stagionalità, tendenze a lungo termine, termini autoregressivi e media mobile al fine di da gestire l’autocorrelazione incorporata nei dati.
Nello smoothing esponenziale le previsioni vengono effettuate sulla base di medie pesate come nei modelli ARMA; ma in questo caso vengono assegnati diversi pesi decrescenti a ciascuna osservazione e, man mano che ci si allontana dal presente, viene data meno importanza alle osservazioni precedenti.
Svantaggi del Machine Learning Tradizionale
E’ risaputo che i modelli di Machine Learning tradizionale presentano molte limitazioni:
- I valori mancanti possono influire molto sulle prestazioni dei modelli
- Non sono in grado di riconoscere pattern complessi all’interno dei dati
- Di solito funzionano bene solamente in previsioni con pochi step nel passato e non in previsioni a lungo termine
Deep Learning per la previsione di serie temporali
L’utilizzo del Deep Learning per la previsione delle serie temporali supera gli svantaggi del Machine Learning tradizionale utilizzando molti approcci diversi. In questo articolo vengono presentate 5 architetture diverse di Deep Learning per la previsione delle serie temporali:
- Recurrent Neural Networks (RNNs) che sono le architetture più classiche e utilizzate per problemi di previsione di serie temporali
- Long Short-Term Memory (LSTM) che sono un’evoluzione delle RNNs sviluppata per superare il problema del gradiente che svanisce (vanishing gradient)
- Encoder-Decoder, modello per RNNs introdotto per risolvere i problemi in cui le sequenze in ingresso hanno una lunghezza diversa da quelle in uscita
- Meccanismo dell’attenzione, evoluzione del modello Encoder-Decoder sviluppato in modo da evitare di dimenticare le parti precedenti di una sequenza
Recurrent Neural Netorks (reti neurali ricorrenti)
RNN sono reti di nodi simili a neuroni organizzati in livelli successivi con un’architettura simile a quella di una rete neurale standard. Di fatti, come nelle reti neurali standard, i neuroni sono divisi in un livello di input, livelli nascosti e livello di output. Ciascuna connessione tra neuroni ha un proprio peso corrispondente che viene imparato dalla rete durante l’addestramento.
La differenza è che in questo caso a ciascun neurone viene assegnato uno step temporale fisso. I neuroni nel livello nascosto sono anche collegati secondo una direzione tempo-dipendente, ovvero ciascuno è completamente connesso solamente con i neuroni di un livello nascosto con lo stesso step temporale assegnato ed è connesso tramite legame unidirezionale ad ogni altro neurone assegnato allo step temporale successivo. I neuroni che ricevono l’input e quelli che ricevono l’output sono connessi solamente ai livelli nascosti con lo stesso step temporale assegnato.
Siccome l’output di un livello nascosto ad un certo step temporale costituisce parte dell’input dello step successivo, l’attivazione dei neuroni è calcolata in ordine di tempo: ad ogni step temporale solamente i neuroni ad esso assegnati calcolano la propria attivazione.
Architettura
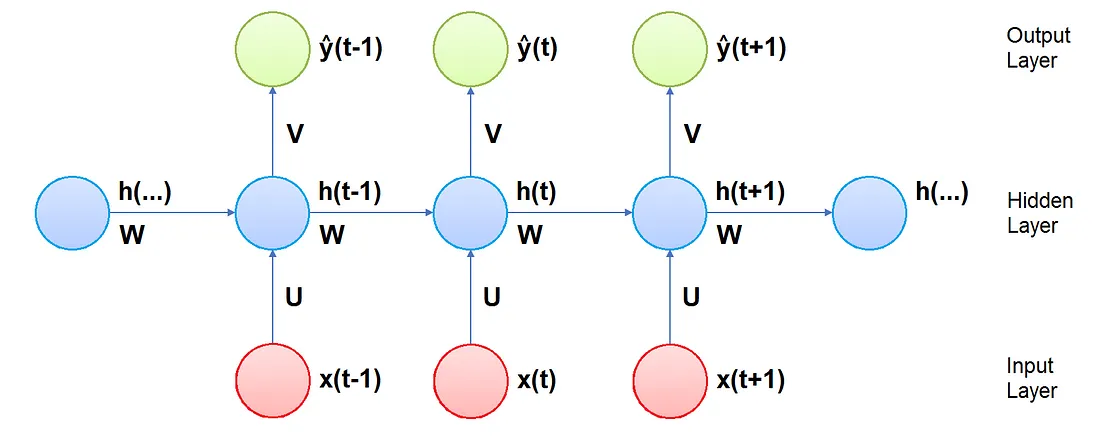
- Pesi: nelle RNNs il vettore in input al tempo t è connesso ai neuroni del livello nascosto al tempo t da una matrice di pesi U. I neuroni nel livello nascosto sono connessi a quelli ai tempi t+1 e t-1 da una matrice di pesi W. I neuroni del livello nascosto sono poi connessi al vettore in output al tempo t da una matrice di pesi V. Tutte le matrici dei pesi sono costanti ad ogni step temporale
- Input: il vettore x(t) è l’input della rete al passo temporale t
- Stato nascosto: il vettore h(t) rappresenta lo stato nascosto al tempo t ed è una sorta di memoria della rete. Viene calcolato sulla base dell’input corrente e degli stati nascosti agli step di tempo passati
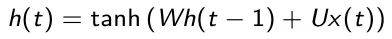
- Output: il vettore y(t) è l’output della rete al tempo t
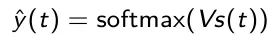
Algoritmo di apprendimento
L’obiettivo del processo di apprendimento è quello di trovare le matrici dei pesi U, V e W migliori possibile, ovvero che permettono di ottenere la previsione y(t) migliore partendo da x(t) come input.
A tal scopo definiamo una funzione detta funzione di perdita e indicata con J che quantifica la distanza tra il valore vero e quello predetto su tutto il training set. Questa funzione è data da:
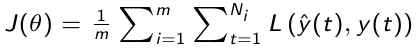
Dove
- la funzione di perdita L valuta la differenza tra valore vero e reale in un singolo step temporale
- m è la dimensione del training set
- θ è il vettore dei parametri del modello
La funzione di perdita J viene minimizzata utilizzando questi due step principali: propagazione in avanti e propagazione indietro nel tempo. Questi step vengono iterati più volte, il numero di iterazioni è detto numero di epoche.
Propagazione in avanti: con parametri U, W e V fissati i dati vengono propagati all’interno della rete e ad ogni istante t si calcola y(t) utilizzando le formule definite precedentemente. Alla fine si può calcolare la funzione di perdita.
Propagazione indietro nel tempo: i gradienti della funzione di perdita sono calcolati rispetto a diversi parametri che vengono poi successivamente aggiornati tramite un algoritmo discendente. I gradienti ottenuti per ogni output dipendono sia da elementi dello stesso step temporale che dallo stato della memoria allo step temporale precedente.
Vantaggi e svantaggi delle reti neurali ricorrenti
In generale le RNNs risolvono molti problemi dei modelli di Machine Learning tradizionale adottati per la previsione di serie temporali
- Le prestazioni delle RNN non sono influenzate in modo significativo dai valori mancanti
- Le RNN sono in grado di trovare pattern complessi nelle serie temporali in ingresso
- Le RNN permettono di ottenere buoni risultati nel prevedere anche step più lunghi nel tempo
- Le RNN possono modellare sequenze di dati in modo che ciascun campione possa essere considerato come dipendente da quelli precedenti
Svantaggi:
- Quando vengono addestrate su serie temporali molto lunghe, le RNN soffrono tipicamente del problema del gradiente che svanisce o che esplode, ovvero i parametri dei livelli nascosti o non cambiano significativamente o portano ad instabilità numerica e comportamento caotico. Questo succede quando il gradiente della funzione di costo include la potenza di W che influisce sulle capacità di memorizzazione
- Le reti ricorrenti intrinseche descritte in precedenza soffrono di una memoria debole incapace di considerare molti elementi nel passato nella predizione del futuro.
- L’addestramento di una rete neurale ricorrente è difficile da parallelizzare ed è anche costoso dal punto di vista computazionale
A fronte di questi svantaggi, sono state progettate diverse estensioni delle RNN in modo da tagliare la memoria interna: reti neurali bidirezionali, LSTM, GRU, meccanismi dell’attenzione. L’ampliamento della memoria può essere cruciale in certi ambiti come la finanza dove è fondamentale ricordare quanta più storia possibile per prevedere gli step successivi.
LSTM
Le reti a memoria a memoria a lungo e breve termine (Long short-term memory networks, LSTM) sono state sviluppate per superare il problema del gradiente che svanisce nelle RNN standard. Il problema viene superato migliorando il flusso del gradiente all’interno della rete. Ciò si ottiene utilizzando un’unità LSTM al posto del livello nascosto. Come mostrato nella figura sottostante, un’unità LSTM è composta da:
- Una cella di stato (cell state) che porta l’’informazione lungo l’intera sequenza e rappresenta la memoria della rete
- Una porta di oblio (forget gate) che decide cosa è rilevante conservare degli step temporali precedenti
- Una porta di ingresso (input gate) che decide quale informazione dello step corrente è rilevante aggiungere
- Una porta di uscita (output gate) che decide il valore dell’output allo step temporale corrente
Similmente alle RNNs, il vettore in input al tempo t è connesso alla cella LSTM del tempo t da una matrice di pesi U. La cella LSTM è connessa alla cella al tempo t-1 e a quella al tempo t+1 da una matrice di pesi W. Infine, la cella LSTM è connessa al vettore di uscita al tempo t da una matrice di pesi V. Le matrici W e U sono divise in sottomatrici (Wf, Wi, Wg, Wo; Uf, Ui, Ug, Uo) connesse a diversi elementi dell’unità LSTM, come mostrato nella figura qua sotto. Tutte le matrici di pesi sono condivise nel tempo.
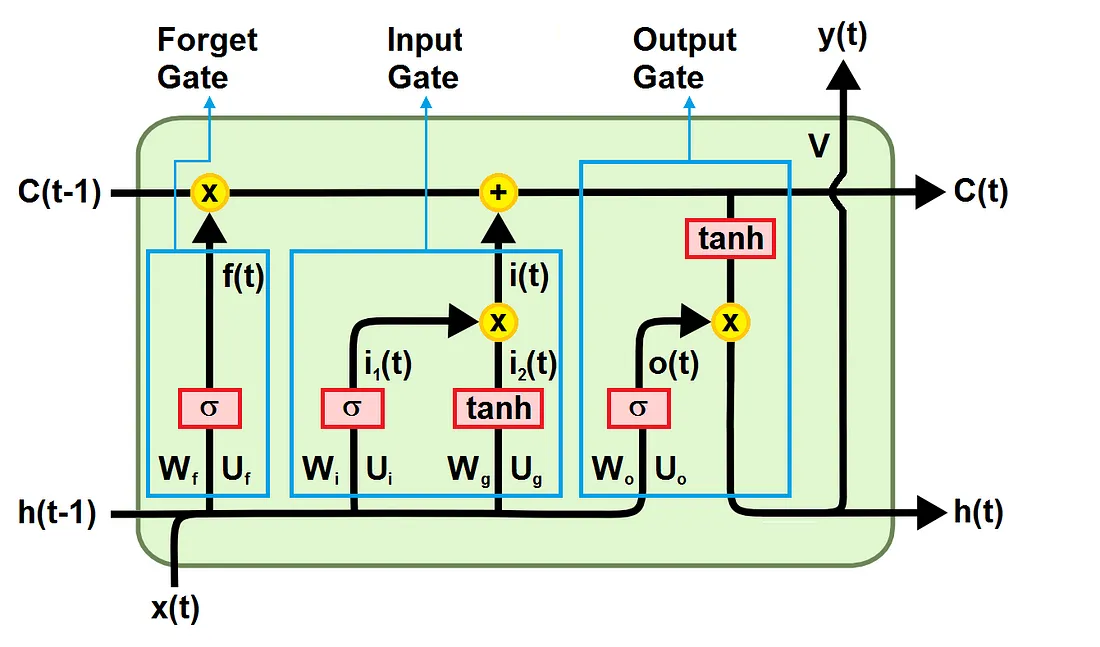
Lo stato della cella trasferisce le informazioni rilevanti durante l’elaborazione in modo che anche l’informazione dai tempi precedenti arrivi ad ogni step temporale, riducendo l’effetto della memoria a breve termine. Durante l’addestramento per tutti gli step temporali le porte imparano quale informazione è importante conservare e quale, invece, dimenticare. L’informazione è quindi aggiunta allo stato della cella o viene rimossa da esso.
In questo modo le LSTM permettono di recuperare dati trasferiti in memoria, risolvendo il problema del gradiente che svanisce. Le LSTM sono utili per classificare, elaborare e prevedere serie temporali con ritardi temporali di durata non nota.
Porta d’oblio
Questa porta decide quale informazione dovrebbe essere rimossa e quale, invece, salvata. L’informazione dallo stato nascosto precedente e quella dell’input corrente vengono inserite in una funzione sigmoide. Un’uscita vicina a 0 significa che l’informazione può essere dimenticata mentre un’uscita vicina a 1 significa che dev’essere salvata.
![]()
Porta di ingresso
Questa porta viene utilizzata per aggiornare lo stato della cella. Inizialmente lo stato nascosto precedente e quello corrente vengono usati come input ad una funzione sigmoide (più l’output è vicino a 1 e più l’informazione è importante). Inoltre, stato nascosto e input corrente vengono inseriti in una funzione tanh per comprimere i valori tra -1 e 1 in modo da migliorare la sintonizzazione della rete. Successivamente, l’uscita della tanh e della sigmoide vengono moltiplicate elemento per elemento (nella formula sottostante il simbolo * indica la moltiplicazione elemento per elemento di due matrici). L’uscita della sigmoide decide quale informazione è importante mantenere dall’uscita della tanh.
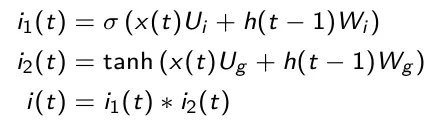
Stato della cella
Dopo l’attivazione della porta di ingresso, è possibile calcolare lo stato della cella. Innanzitutto, lo stato della cella del passo temporale precedente viene moltiplicato elemento per elemento per l’uscita della porta di oblio. Ciò dà la possibilità di ignorare i valori nello stato della cella quando sono moltiplicati per valori prossimi a 0. Poi l’uscita della porta di ingresso viene aggiunta elemento per elemento allo stato della cella. L’output è il nuovo stato della cella.
![]()
Porta di uscita
La terza e ultima porta è quella di uscita che decide il valore del prossimo stato nascosto il quale contiene informazioni riguardo agli ingressi precedenti. Innanzitutto, lo stato nascosto precedente e l’ingresso corrente vengono sommati e passati a una funzione sigmoide. Poi il nuovo stato nascosto viene passato alla funzione tanh. Alla fine, l’uscita tanh e l’uscita sigmoide vengono moltiplicate per decidere quali informazioni lo stato nascosto debba contenere. Il risultato è il nuovo stato nascosto. Il nuovo stato della cella e il nuovo stato nascosto vengono portati allo step temporale successivo.
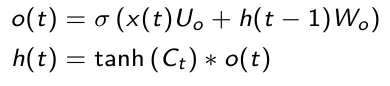
Gated Recurrent Unit (GRU)
La GRU rappresenta una nuova generazione di reti neurali ricorrenti ed è molto simile alla LSTM. Per risolvere il problema del gradiente che svanisce in una RNN standard, la GRU utilizza la porta di aggiornamento e la porta di reset. Ovvero, due porte che decidono quali informazioni devono essere passate all’uscita. Queste due porte possono essere addestrate per mantenere le informazioni di molti passi temporali precedenti quello attuale, senza che vengano dimenticate nel tempo, oppure per rimuovere le informazioni irrilevanti per la previsione.Se addestrata adeguatamente, la GRU può avere prestazioni assolutamente ottime anche negli scenari più complessi.
Come mostrato nella figura seguente, un’unità GRU è composta da:
- Una porta di reset che decide quanto delle informazioni dagli step temporali precedenti debbano essere dimenticate
- Una porta di aggiornamento che quanto delle informazioni dagli step temporali precedenti debbano essere salvate
- Una memoria che mantiene le informazioni lungo l’intera sequenza e rappresenta la memoria della rete
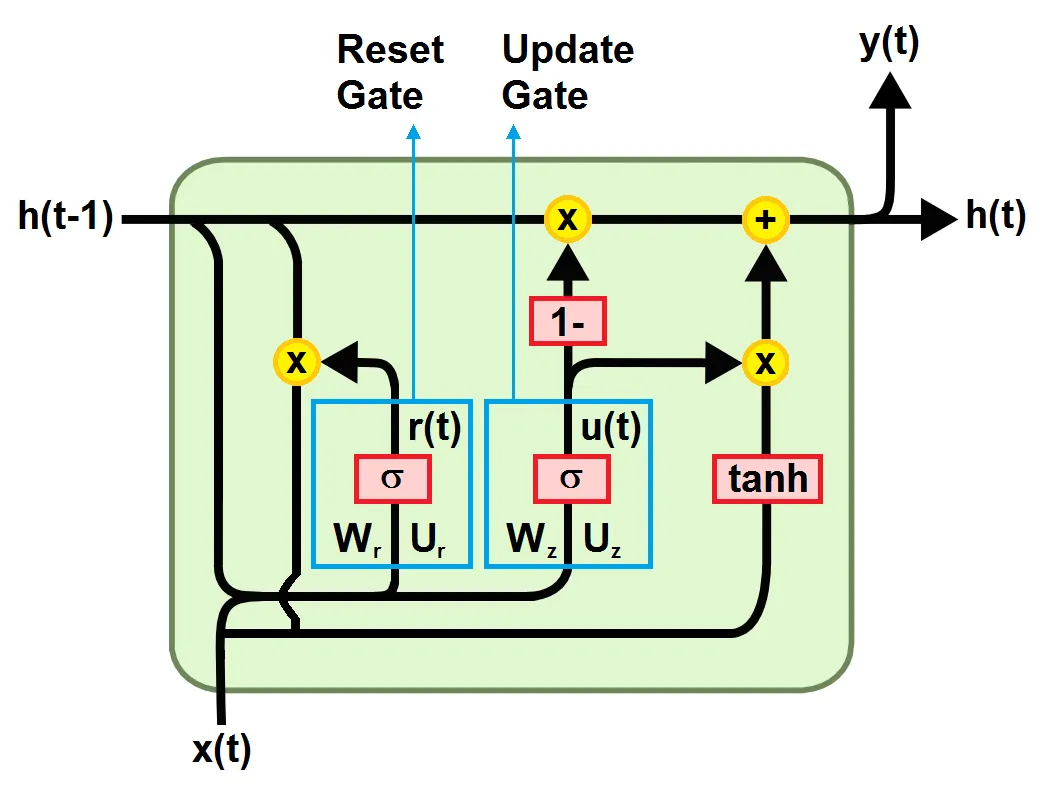
Porta di reset
Determina come combinare il nuovo input con la memoria precedente, decidendo quanta parte delle informazioni dei passi temporali precedenti può essere dimenticata. Per prima cosa viene eseguita la somma pesata tra l’ingresso x(t) e la memoria h(t-1), che contiene le informazioni dei precedenti t-1 passi. Poi viene applicata una funzione di attivazione sigmoide per comprimere il risultato tra 0 e 1.
![]()
Porta di aggiornamento
Aiuta il modello a determinare quanta parte delle informazioni dei passi temporali precedenti debba essere trasmessa agli step successivi. Si tratta di una funzione molto potente, perché il modello può decidere di copiare tutte le informazioni dal passato, eliminando il rischio del problema del gradiente che svanisce. La formula per calcolarla è analoga a quella della porta di reset, ma la differenza sta nei pesi e nell’uso della porta (sarà chiaro nel calcolo della memoria).
![]()
Memoria corrente
Il contenuto della memoria utilizza la porta di reset per memorizzare le informazioni rilevanti del passato. Per ottenere ciò, prima viene calcolata la moltiplicazione elemento per elemento tra l’uscita della porta di reset r(t) e la memoria finale allo step temporale precedente h(t-1). Poi la somma pesata tra il risultato e l’ingresso x(t) viene eseguita. Infine, la funzione di attivazione non lineare tanh viene applicata.
![]()
Memoria finale
Come ultima cosa, la rete deve calcolare h(t), che è il vettore che contiene le informazioni per l’unità corrente e le passa allo step temporale successivo. Determina cosa raccogliere dal contenuto della memoria corrente h~(t) e cosa dagli step precedenti h(t-1). Viene calcolato facendo la moltiplicazione elemento per elemento tra la porta di aggiornamento z_t e h_(t-1), e tra (1-z_t) e h~(t). Infine viene calcolata la somma pesata yhr tra i due risultati.
![]()
Implementazione di RNN, LSTM e GRU
QUeste reti possono essere implementate utilizzando l’API di Keras che sono progettate in modo da essere facili da utilizzare e personalizzabili. In Keras sono presenti le seguenti 3 RNN:
- keras.layers.SimpleRNN
- keras.layers.LSTM
- keras.layers.GRU
Permettono di creare velocemente template ricorrenti senza dover fare scelte di configurazione complesse. In aggiunta è possibile definire un livello di cella RNN con un comportamento desiderato, permettendo di testare rapidamente vari prototipi diversi in modo flessibile e con codice minimo. Sul sito web di Tensorflow è possibile trovare istruzioni e molti esempi di utilizzo di questi livelli.
Modello Encoder-Decoder
Nelle RNN, LSTM, GRU ogni ingresso corrisponde a un’uscita per lo stesso passo temporale. Tuttavia, in molti casi reali si vuole prevedere una sequenza di output utilizzando una sequenza di input di lunghezza diversa, senza quindi avere necessariamente corrispondenza tra ciascun input e ciascun output. Questa situazione viene chiamata modello di mappatura sequenza-sequenza ed è alla base di numerose applicazioni di uso comune, come ad esempio le traduzioni linguistiche, i dispositivi vocali e i chatbot online.
Il modello Encoder-Decoder per le reti neurali ricorrenti è stato introdotto per affrontare i modelli di mappatura sequenza-sequenza. Un Encoder-Decoder prende in ingresso una sequenza e come output genera la sequenza successiva più probabile. Come suggerisce il nome, il modello è costituito da due sottomodelli:
- l’encoder ha la responsabilità di scorrere gli step temporali in ingresso e di codificare l’intera sequenza in un vettore di lunghezza fissa chiamato vettore di contesto;
- il decoder ha la responsabilità di scorrere gli step temporali di uscita leggendo il vettore di contesto
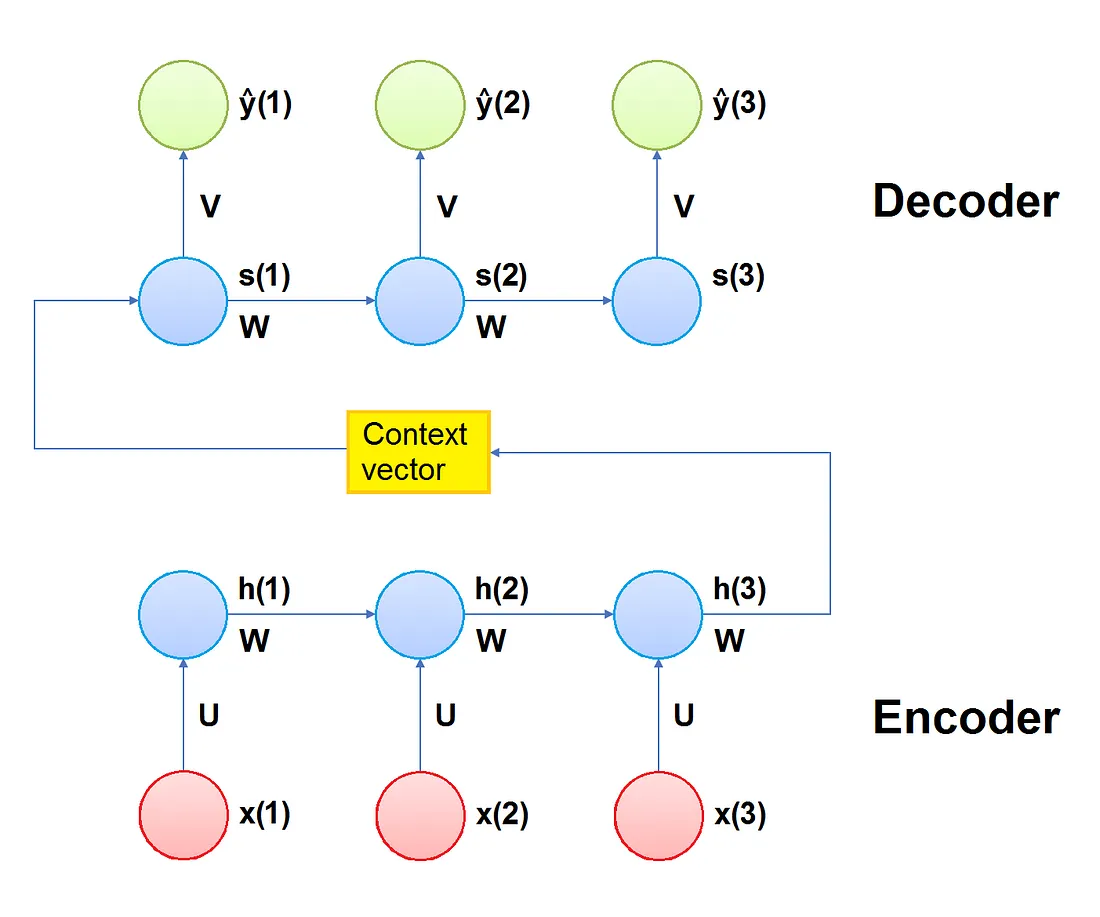
Encoder
L’encoder è costituito da una serie di diverse unità ricorrenti che possono essere semplici RNN, celle LSTM o celle GRU. Ogni unità accetta un singolo elemento della sequenza di ingresso, raccoglie informazioni da quell’elemento e le propaga in avanti.
Il vettore di stato nascosto h(t) viene calcolato utilizzando la funzione dell’unità ricorrente scelta. La funzione viene applicata con i pesi appropriati allo stato nascosto precedente h(t-1) e al vettore di ingresso x(t):
![]()
Vettore di contesto
Il vettore di contesto è lo stato nascosto finale prodotto dalla parte codificante (encoder) del modello e rappresenta lo stato nascosto iniziale per il decoder. Racchiude le informazioni relative a tutti gli elementi in ingresso per aiutare il decodificatore a fare previsioni accurate.
Decoder
Il decoder consiste in una serie di diverse unità ricorrenti. Ciascuna accetta uno stato nascosto s(t-1) dall’ unità precedente e produce un output y(t) insieme al proprio stato nascosto s(t).
Lo stato nascosto s(t) viene calcolato in base alla funzione dell’unità ricorrente scelta:
![]()
L’uscita y(t) viene calcolata utilizzando la funzione softmax e lo stato nascosto allo step temporale corrente s(t) insieme al rispettivo peso. Ciò al fine di creare un vettore di probabilità:
![]()
Meccanismo di attenzione
Il meccanismo di attenzione è una delle principali frontiere del Deep Learning ed è un’evoluzione del modello Encoder-Decoder, sviluppato per migliorare le prestazioni su lunghe sequenze di input.
L’idea principale è quella di consentire al decoder di accedere selettivamente alle informazioni dell’encoder durante la decodifica. Ciò si ottiene costruendo un vettore di contesto diverso per ogni passo temporale del decoder, calcolandolo in funzione dello stato nascosto precedente e di tutti gli stati nascosti dell’encoder, assegnando loro pesi addestrabili.
In questo modo, il meccanismo dell’attenzione assegna diversa importanza ai diversi elementi della sequenza in ingresso, dando maggiore attenzione a quelli più rilevanti. (Questo spiega il nome del modello).
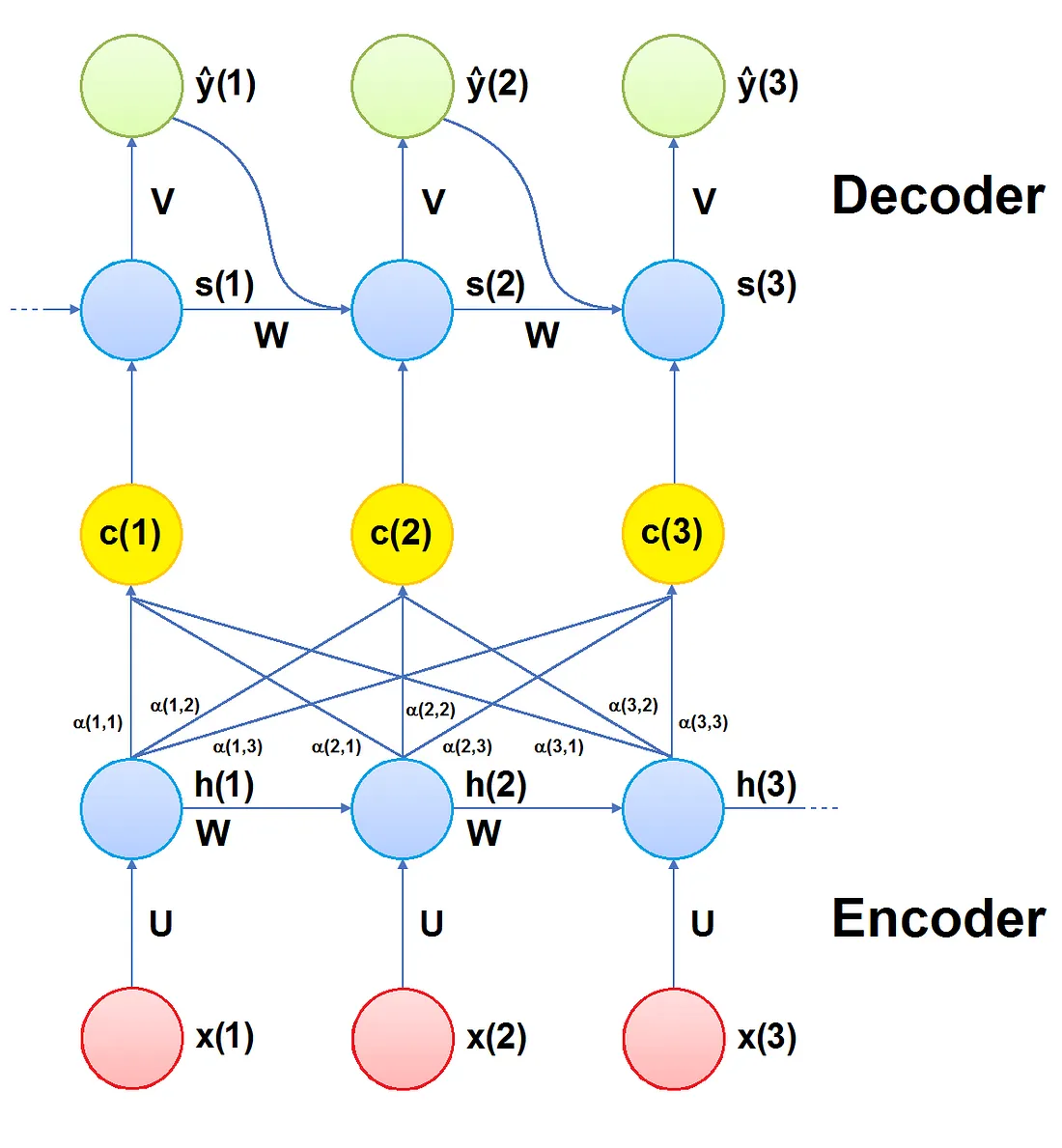
Encoder
Il funzionamento dell’encoder è molto simile a quello che segue la parte di codifica di un encoder-decoder. Ad ogni step temporale, ogni input viene rappresentato come funzione dello stato nascosto dello step temporale precedente e di quello corrente. Lo stato finale nascosto contiene tutte le informazioni codificate dalle rappresentazioni precedenti e dagli ingressi precedenti.
![]()
Vettore di contesto
La differenza principale tra il meccanismo di attenzione e il modello Encoder-Decoder è che un vettore di contesto c(t) diverso viene calcolato ad ogni step temporale del decoder.
Per calcolare il vettore di contesto c(t) per il passo temporale t si procede come segue. Innanzitutto, per ogni combinazione di step temporale j dell’encoder e ogni step temporale t del decoder, i cosiddetti punteggi di allineamento e(j,t) vengono calcolati con la seguente somma ponderata:
![]()
In questa equazione, Wₐ, Uₐ e Vₐ sono pesi addestrabili, chiamati pesi di attenzione. I pesi Wₐ sono associati agli stati nascosti dell’encoder, i pesi Uₐ sono associati agli stati nascosti del decoder e i pesi Vₐ definiscono la funzione che calcola il punteggio di allineamento.
Per ogni passo temporale t, i punteggi e(j,t) vengono normalizzati utilizzando la funzione softmax sui passi temporali j dell’encoder, ottenendo i pesi di attenzione α(j,t):
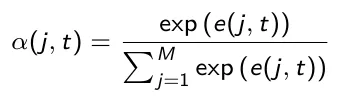
Il peso di attenzione α(j,t) cattura l’importanza dell’ingresso allo step temporale j per decodificare l’uscita al tempo t. Il vettore di contesto c(t) viene calcolato come somma pesata di tutti i valori nascosti dell’encoder in base ai pesi di attenzione:

Questo vettore di contesto permette di dare più attenzione agli ingressi più rilevanti della sequenza in input.
Decoder
Ora il vettore di contesto c(t) viene passato al decoder, che calcola la distribuzione di probabilità del prossimo output possibile. Questa operazione di decodifica avviene per tutti i passi temporali presenti nell’input.
Poi, lo stato nascosto attuale s(t) viene calcolato in base alla funzione di unità ricorrente, considerando come input il vettore di contesto c(t), lo stato nascosto s(t-1) e l’output y(t-1) dello step temporale precedente:
![]()
Per cui utilizzando questo meccanismo il modello è in grado di identificare correlazioni tra diverse parti della sequenza in ingresso e le corrispondenti parti di quella in uscita.
Ad ogni step temporale l’uscita del decoder è calcolata applicando la funzione softmax allo stato nascosto pesato:
![]()
Vantaggi
Come già detto, il meccanismo di attenzione dà buoni risultati anche in presenza di lunghe sequenze di input.
- Grazie ai pesi di attenzione, il meccanismo di attenzione ha anche il vantaggio di essere più interpretabile rispetto ad altri modelli di Deep Learning che sono generalmente considerati come ‘scatole nere’ visto che non hanno la capacità di spiegare i propri output
- Inoltre, il meccanismo di attenzione dà risultati eccezionali nei modelli NLP, poiché consente di ricordare tutte le parole presenti in ingresso e di riconoscere le parole più rilevanti durante la formulazione di una risposta
Implementazione
Il meccanismo dell’attenzione può essere sviluppato usando TensorFlow e Keras e facilmente integrato in altri livelli di keras. Su Github si possono trovare svariate implementazioni, per esempio:
https://github.com/uzaymacar/attention-mechanisms
https://github.com/philipperemy/keras-attention-mechanism
A questi link potete trovare moltissimi esempi sulla classificazione dei sentimenti, generazione di testo, classificazione di documenti e traduzione automatica.
Conclusioni
Le Reti Neurali Ricorrenti sono la tecnica di Deep Learning più utilizzata per la previsione delle serie temporali, in quanto permettono di ottenere previsioni affidabili su serie temporali appartenenti a problemi di tipo diverso.
Il problema principale delle RNN è che soffrono del problema del gradiente che svanisce quando vengono applicate a sequenze lunghe.
LSTM e GRU sono state create per mitigare il problema del gradiente che svanisce delle RNN tramite l’uso di porte che regolano il flusso di informazioni attraverso la catena di sequenze.
L’uso di LSTM e GRU dà risultati notevoli quando impiegato in applicazioni come il riconoscimento vocale, la sintesi vocale, la comprensione del linguaggio naturale, ecc.
Il modello Encoder-Decoder per le reti neurali ricorrenti è la tecnica più comune per i problemi di mappatura sequenza-sequenza in cui le sequenze di ingresso hanno una lunghezza diversa rispetto a quelle in uscita.
Il meccanismo dell’attenzione è un’evoluzione del modello Encoder-Decoder, per risolvere la riduzione delle prestazioni in caso di lunghe sequenze. Ciò si ottiene utilizzando un vettore di contesto diverso per ogni passo temporale I risultati ottenuti per diverse aree sono notevoli, ad esempio NLP, classificazione di sentimenti, classificazione di documenti ecc.
L’autore
Articoli su Towards Data Science: https://medium.com/@marcodelpra
Profilo Linkedin: https://www.linkedin.com/in/marco-del-pra-7179516/
Gruppo Linkedin AI Learning: https://www.linkedin.com/groups/8974511/
Share:


