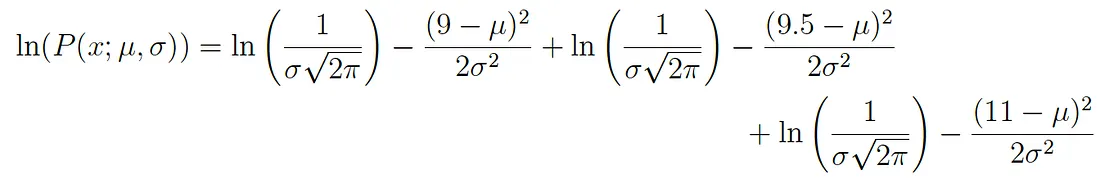Concetti di probabilità spiegati: la stima della massima verosimiglianza
Introduzione
Articolo in lingua originale di Jonny Brooks-Bartlett

In questo post spiegherò cos’è il metodo della massima verosimiglianza per la stima dei parametri e illustrerò un semplice esempio per dimostrare il metodo. Alcuni contenuti richiedono la conoscenza di concetti fondamentali di probabilità, come la definizione di probabilità congiunta e l’indipendenza degli eventi. Ho scritto un post sul blog con questi prerequisiti, quindi non esitate a leggerlo se pensate di aver bisogno di un ripasso.
Cosa sono i parametri?
Spesso nel Machine Learning si utilizza un modello per descrivere il processo che porta ai dati osservati. Per esempio, possiamo usare un modello random forest per classificare se i clienti possono cancellare un abbonamento da un servizio (noto come churn modelling) o potremmo usare un modello lineare per prevedere le entrate generate per un’azienda a seconda di quanto questa investe nella pubblicità (questo è un esempio di regressione lineare). Ogni modello è definito da una serie di parametri.
Un modello lineare lo possiamo scrivere come y = mx + c. In questo esempio x potrebbe rappresentare la quantità di soldi spesa in pubblicità mentre y potrebbe rappresentare il guadagno generato. Associare valori diversi a questi parametri significa ottenere rette diverse (vedi figura qua sotto)

Quindi i parametri definiscono uno schema per il modello. Solamente quando vengono scelti valori specifici ei parametri che si ottiene un’istanziazione del modello che descrive un certo fenomeno.
Spiegazione intuitiva della stima della massima verosimiglianza
La stima della massima verosimiglianza è un metodo che determina i valori dei parametri di un modello. I valori dei parametri vengono trovati in modo da massimizzare la probabilità che il processo descritto dal modello abbia prodotto i dati effettivamente osservati.
Questa definizione potrebbe sembrare ancora un po’ criptica, quindi facciamo un esempio per capirla meglio.
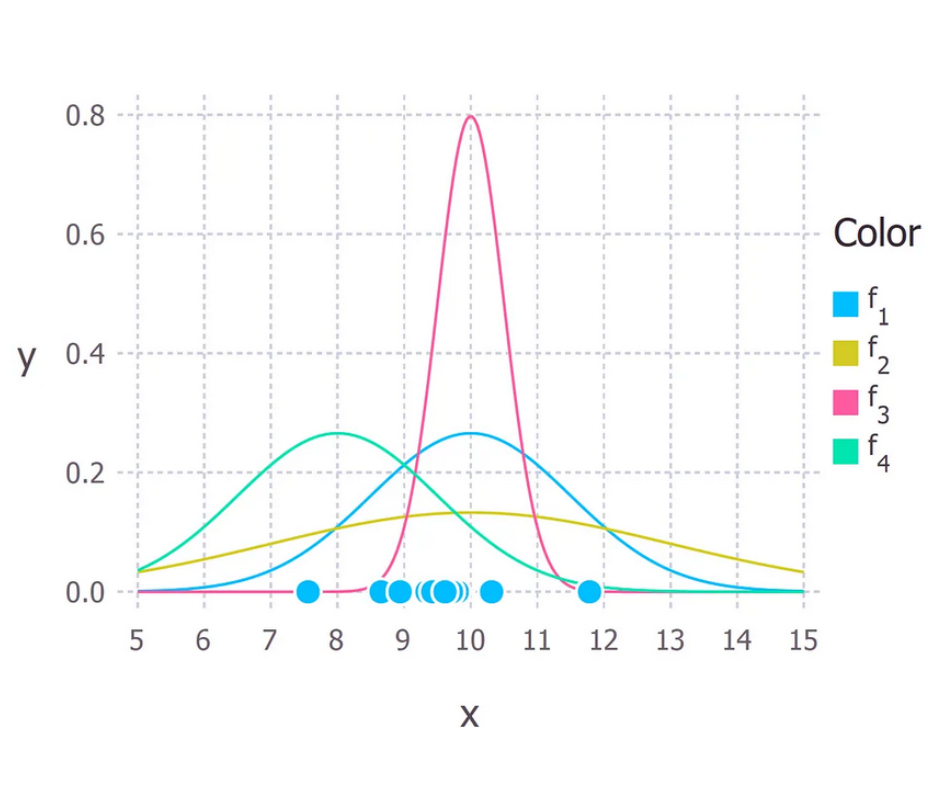
Supponiamo di aver osservato 10 realizzazioni di un certo processo. Ad esempio, ogni punto potrebbe rappresentare il tempo in secondi che ci mette uno studente a rispondere ad una domanda d’esame specifica. Questi 10 punti sono mostrati nella figura seguente

Dobbiamo innanzitutto decidere quale modello riteniamo descriva meglio il processo di generazione dei dati. Questa parte è molto importante. Come minimo, dovremmo avere una buona idea del modello da utilizzare. Di solito ciò deriva da una certa esperienza riguardo al dominio a cui appartiene il problema, ma non ne parleremo in questa occasione.
Assumiamo per questi dati che il processo che li ha generati possa essere descritto adeguatamente da una distribuzione normale (Gaussiana). Guardando la figura sopra, una distribuzione gaussiana è plausibile in quanto la maggior parte dei punti sono raggruppati al centro mentre pochi si posizionano a destra o a sinistra. (Prendere questo tipo di decisione al volo con soli 10 punti è sconsigliabile, tuttavia siccome ho generato io questi punti ci accontentiamo).
Si ricorda che la distribuzione Gaussiana ha 2 parametri: la media, μ, e la deviazione standard, σ. Valori diversi di questi parametri danno luogo a curve diverse (proprio come nel caso delle linee rette di cui sopra). Vogliamo sapere quale curva è più probabile che abbia creato i dati osservati. (Vedi figura sotto). La stima della massima verosimiglianza è un metodo in grado di trovare i valori di μ e σ che definiscono la curva che fitta meglio i dati.

La vera distribuzione da cui sono stati generati i dati è f1 ~ N(10, 2,25), che rappresenta la curva blu nella figura precedente.
Calcolare le stime della massima verosimiglianza
Ora che abbiamo capito in modo intuitivo cosa significa stima della massima verosimiglianza possiamo passare ad imparare come calcolare i valori dei parametri. I valori che troviamo vengono chiamati stime della massima verosimiglianza.
Procediamo con un esempio anche in questo caso. Supponiamo questa volta di avere tre campioni e assumiamo che siano stati generati da un processo descritto adeguatamente da una distribuzione gaussiana. Questi punti sono 9, 9,5 e 11. Come si calcolano le stime di massima verosimiglianza dei valori dei parametri μ e σ della distribuzione gaussiana?
Quello che vogliamo calcolare è la probabilità totale di osservare tutti i dati, cioè la distribuzione di probabilità congiunta di tutti i dati osservati. Per farlo, avremo bisogno di calcolare alcune probabilità condizionate, il che può risultare molto difficile. Ed è qui che facciamo la nostra prima ipotesi, ovvero che ciascun dato è generato indipendentemente dagli altri. Questo rende la matematica molto più semplice. Se gli eventi (cioè il processo che genera i dati) sono indipendenti, allora la probabilità totale di osservare tutti i dati equivale a moltiplicare tra loro le probabilità di osservare ciascun punto individualmente (cioè il prodotto delle probabilità marginali).
La densità di probabilità di osservare un singolo punto x generato da una distribuzione gaussiana è data da:
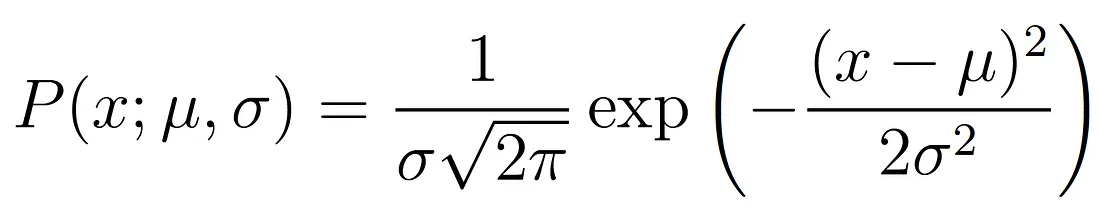
Il punto e virgola utilizzato nella notazione P(x; μ, σ) serve a sottolineare che i simboli che compaiono dopo di esso sono parametri della distribuzione di probabilità. Non va quindi confusa con la probabilità condizionata (che viene tipicamente rappresentata con una linea verticale, ad esempio P(A| B)).
Nel nostro esempio la densità di probabilità totale (congiunta) di osservare i tre punti è data da:
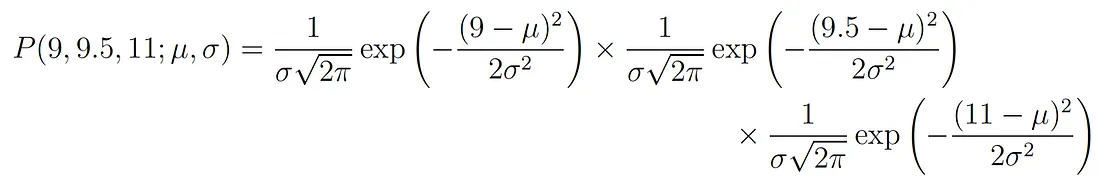
Dobbiamo solo trovare i valori di μ e σ che portano ad avere il massimo valore dell’espressione riportata sopra.
Se avete un po’ di basi di matematica, probabilmente saprete che c’è una tecnica che ci può aiutare a trovare i massimi e i minimi di una funzione, ovvero la derivazione. Tutto quello che dobbiamo fare è trovare la derivata della funzione, impostare la derivata uguale a zero e riorganizzare l’equazione in modo da ricavare il parametro di interesse. E voilà! Abbiamo i nostri valori MLE per i nostri parametri. Passerò ora in rassegna questi step, ma assumerò che il lettore conosca come calcolare la derivata delle funzioni più comuni.
La verosimiglianza logaritmica
L’espressione sopra riportata per la probabilità totale è in realtà piuttosto complicata da derivare, viene quindi semplificata considerandone il logaritmico. Questo è lecito in quanto il logaritmo naturale è una funzione monotonicamente crescente. Ciò significa che se il valore dell’ascissa (x) aumenta, allora aumenta anche y (vedi figura sottostante). Questo è importante perché assicura che il massimo valore della probabilità logaritmica si verifica nello stesso punto della funzione di probabilità originale. Pertanto possiamo lavorare con la verosimiglianza logaritmica invece che con quella originale.


Considerando il logaritmo dell’espressione originale otteniamo:
Questa espressione può essere semplificata ulteriormente seguendo le leggi dei logaritmi in modo da ottenere:
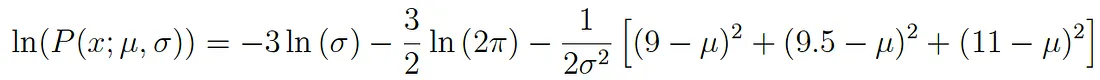
Questa espressioen può essere derivata in modo da trovare il massimo. In questo esempio troveremo il MLE della media, μ. PEr poterlo fare dobbiamo considerare la derivata parziale della funzione rispetto a μ, ottenendo quindi:
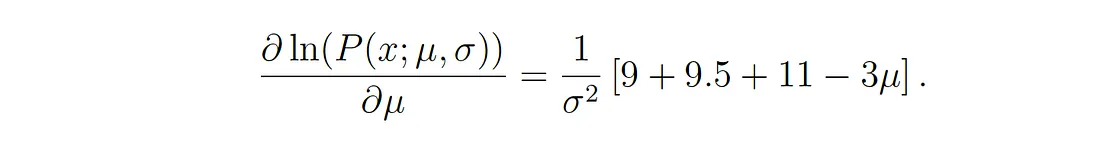
Infine, impostando la porzione a sinistra dell’equazione uguale a zero e riorganizzando i valori, si ottiene:
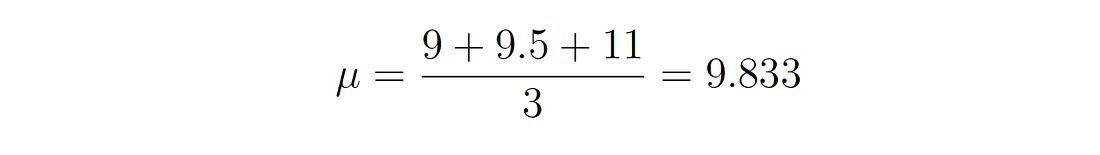
Ed ecco che otteniamo la stima della massima verosimiglianza per μ. Possiamo fare la stessa cosa anche con σ ma lascerò questa parte come esercizio per i lettori più appassionati.
Considerazioni finali
L’equazione della stima della massima verosimigliaza può essere sempre risolta in modo esatto?
In breve la risposta è no. In uno scenario reale è molto più probabile che la derivata della funzione logaritmica rimanga comunque non trattabile (ad esempio, è troppo difficile/impossibile derivare la funzione a mano). Perciò esistono metodi iterativi come gli algoritmi di expectation-maximization che vengono utilizzati per trovare soluzioni numeriche per le stime dei parametri. L’idea generale rimane, però, la stessa.
Quindi perchè massima verosimiglianza e non massima probabilità?
Beh in realtà riguarda gli statistici che sono pedanti (ma per una buona ragione). La maggior parte delle persone tende a usare probabilità e verosimiglianza in modo intercambiabile, ma gli statistici e i teorici della probabilità distinguono tra le due cose. La ragione di questa confusione è meglio evidenziata osservando l’equazione.
![]()
Queste espressioni sono uguali! Che cosa significa? Definiamo innanzitutto P(dati; μ, σ) che significa “la densità di probabilità di osservare i dati da un modello con parametri μ e σ”. E’ bene far notare che si può generalizzare a qualsiasi numero di parametri e a qualsiasi distribuzione.
D’altra parte, L(μ, σ; dati) significa “la verosimiglianza con cui i parametri μ e σ assumano determinati valori dato che abbiamo osservato una certa serie di dati”.
L’equazione sopra dice che la densità di probabilità dei campioni dati i parametri è uguale alla verosimiglianza dei parametri dati i i campioni. Nonostante queste due considerazioni siano uguali, la verosimiglianza e la probabilità di densità pongono fondamentalmente due domande diverse: una riguarda i dati e l’altra i valori dei parametri. Per questo motivo il metodo si chiama massima verosimiglianza e non massima probabilità.
Quando la minimizzazione dei minimi quadrati è uguale alla stima della massima verosimiglianza?
La minimizzazione dei minimi quadrati è un altro metodo comune per stimare i valori dei parametri di un modello di machine learning. Quando il modello viene assunto Gaussiano come nell’esempio precedente, le stime MLE sono equivalenti al metodo dei minimi quadrati. Per una derivazione matematica più approfondita, guardate queste slide!
Possiamo comprendere intuitivamente il legame tra i due metodi attraverso i loro obiettivi. Per la stima dei parametri dei minimi quadrati vogliamo trovare la retta che minimizza la distanza quadratica totale tra i dati e la retta di regressione (si veda la figura seguente). Nella stima della massima verosimiglianza vogliamo massimizzare la probabilità totale dei dati. Quando si assume una distribuzione gaussiana, la massima probabilità si trova quando i dati si avvicinano al valore medio. Siccome la distribuzione Gaussiana è simmetrica, questo equivale a minimizzare la distanza tra i dati e il valore medio.

Nel prossimo post ho in previsione di coprire l’interferenza Bayesiana e come può essere utilizzata per la stima dei parametri.
Grazie per l’attenzione!
Share: