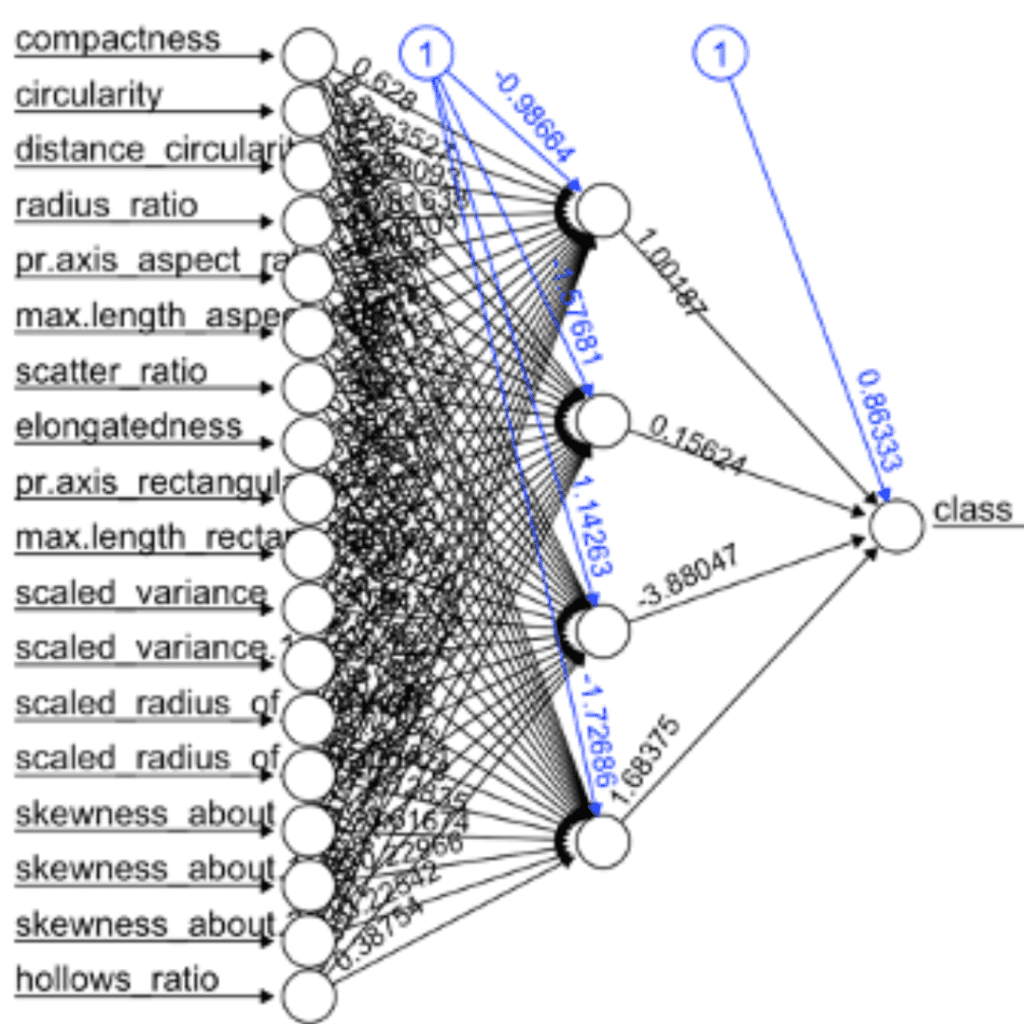
Riduzione della dimensionalità – La PCA migliora davvero il risultato della classificazione?
Introduzione
Articolo originale in lingua inglese di Meigarom
Mi sono imbattuto in un paio di risorse sulle tecniche di riduzione della dimensionalità. Questo argomento è sicuramente uno dei più interessanti, è bello pensare che ci siano algoritmi in grado di ridurre il numero di funzionalità scegliendo le più importanti che ancora rappresentano l’intero set di dati. Uno dei vantaggi indicati dagli autori è che questi algoritmi possono migliorare i risultati del compito di classificazione.
In questo post, ho intenzione di verificare questa affermazione utilizzando un Principal Component Analysis ( PCA ) per cercare di migliorare le prestazioni di classificazione di una rete neurale su un set di dati. Il PCA realmente migliora il risultato di classificazione?
Andiamo a vedere.
Algoritmi di riduzione dimensionale
Prima di passare direttamente al codice, parliamo di algoritmi di riduzione dimensionale. Esistono due algoritmi principali per la riduzione della dimensionalità: Linear Discriminant Analysis ( LDA ) e Principal Component Analysis ( PCA ). La differenza fondamentale tra questi due è che LDA usa le informazioni delle classi per trovare nuove funzionalità al fine di massimizzarne la separabilità mentre PCA usa la varianza di ogni funzione per fare lo stesso. In questo contesto, LDA può essere considerato un algoritmo supervisionato e PCA un algoritmo non supervisionato.
Parlando di PCA
L’idea alla base della PCA è semplicemente quella di trovare un insieme di assi di bassa dimensione che riassumano i dati. Perché abbiamo bisogno di riassumere i dati? Pensiamo a questo esempio: abbiamo un set di dati composto da un insieme di proprietà da auto. Queste proprietà descrivono ogni auto per le sue dimensioni, colore, circolarità, compattezza, raggio, numero di sedili, numero di porte, dimensioni del tronco e così via. Tuttavia, molte di queste caratteristiche misurano le proprietà correlate e quindi saranno ridondanti. Pertanto, dovremmo rimuovere queste ridondanze e descrivere ogni auto con meno proprietà. Questo è esattamente ciò che PCA mira a fare. Ad esempio, pensare al numero di ruote come una caratteristica di automobili e autobus, quasi ogni esempio da entrambe le classi hanno quattro ruote, quindi possiamo dire che questa caratteristica ha una bassa varianza ( da quattro a sei ruote o più in alcuni degli autobus rari ), quindi questa funzione renderà autobus e auto sembrano uguali, ma in realtà sono abbastanza diversi l’uno dall’altro. Ora, considerare l’altezza come una caratteristica, auto e autobus hanno valori diversi per esso, la varianza ha una grande gamma dalla vettura più bassa fino al bus più alto. Chiaramente, l’altezza di questi veicoli è una buona proprietà per separarli. Ricordiamo che PCA non prende le informazioni delle classi in considerazione, basta guardare la varianza di ogni caratteristica perché è ragionevole assume che le caratteristiche che presentano varianza elevata sono più probabilità di avere una buona divisione tra le classi.
Spesso, le persone finiscono per commettere un errore nel pensare che PCA seleziona alcune caratteristiche dal set di dati e ne scarta altre. L’algoritmo in realtà costruisce un nuovo insieme di proprietà in base alla combinazione di quelle vecchie. Matematicamente parlando, PCA esegue una trasformazione lineare spostando l’insieme originale di caratteristiche in un nuovo spazio composto da componente principale. Queste nuove caratteristiche non hanno alcun significato reale per noi, solo algebrico, quindi non credo che combinando linearmente caratteristiche, troverete nuove caratteristiche che non avete mai pensato che potrebbe esistere. Molte persone credono ancora che gli algoritmi di apprendimento automatico siano magici, mettono migliaia di input direttamente nell’algoritmo e sperano di trovare tutte le informazioni e le soluzioni per il loro business. Non farti prendere in giro. È compito dello scienziato dei dati individuare le intuizioni del business attraverso un’analisi esplorativa ben condotta dei dati utilizzando l’algoritmo di apprendimento automatico come un insieme di strumenti e non come una bacchetta magica. Tienilo a mente.
Come figura lo spazio dei componenti principali?
Nel nuovo spazio funzionalità stiamo cercando alcune proprietà che differiscono fortemente tra le classi. Come ho mostrato nell’esempio precedente, alcune proprietà che presentano una bassa varianza non sono utili, renderà gli esempi uguali. D’altra parte, PCA cerca proprietà che mostrino quante più variazioni possibili tra le classi per costruire lo spazio dei componenti principali. L’algoritmo usa i concetti della matrice di varianza, della matrice di covarianza, delle coppie degli autovettori e degli autovalori per eseguire il PCA, fornendo un insieme degli autovettori ed i relativi autovalori rispettivamente come risultato. Come esattamente il PCA effettua è materiale per i prossimi post.
Quindi, cosa dovremmo fare con gli autovalori e gli autovettori? È molto semplice, gli autovettori rappresentano il nuovo insieme di assi dello spazio componente principale e gli autovalori portano le informazioni di quantità di varianza che ogni autovettore ha. Quindi, per ridurre la dimensione del set di dati sceglieremo quegli autovettori che hanno più varianza e scarteremo quelli con meno varianza. Come andiamo però l’esempio qui sotto, sarà sempre più chiaro come esattamente funziona.
Vediamo finalmente un po' di codice.
Ora, abbiamo raggiunto la parte divertente e interessante di questo post. Vediamo se PCA migliora davvero il risultato del compito di classificazione.
Per comprometterlo, la mia strategia è di applicare una rete neurale su un set di dati e vedere i suoi risultati iniziali. Successivamente, eseguirò la PCA prima della classificazione e applicherò la stessa rete neurale sul nuovo set di dati e infine confronterò entrambi i risultati.
Il set di dati ha origine dal repository di machine learning UCI chiamato “Statlog ( Vehicle Silhouettes ) dataset”. Questo set di dati memorizza alcune misure di quattro silhouettes dei veicoli con lo scopo di classificazione. È composto da 946 esempi e 18 misure ( attributi ) tutti i valori numerici, è possibile controllare maggiori dettagli qui in questo link: https://archive.ics.uci.edu/ml/datasets/Statlog+(Vehicle+Silhouettes). La rete neurale sarà un Perceptron multistrato con quattro nodi nascosti e un nodo di uscita, tutti con funzione sigmoide come funzione di attivazione e funzioni PCA provenienti da un pacchetto R.
Preparazione del set di dati
Prima di tutto, preparerò il set di dati per la classificazione binaria.
Selezionerò esempi solo da due classi per comporre una classificazione binaria. Gli esempi verranno da classi “bus” e “Saab”. La classe “Saab” sarà sostituita dalla classe 0 e la classe “bus” sarà sostituita dalla classe 1. Il passo successivo consiste nel separare il set di dati in set di dati di formazione e test con il 60% e il 40% degli esempi di classe totali, rispettivamente.
Dopo la precedente preparazione del dataset, modelliamo una rete neurale usando tutte le funzionalità contemporaneamente e poi applichiamo il set di dati di test.
# Load library library( dplyr ) # Load dataset data = read.csv( "../dataset/vehicle.csv", stringsAsFactor = FALSE ) # Transform dataset dataset = data %>% filter( class == "bus" | class == "saab" ) %>% transform( class = ifelse( class == "saab", 0, 1 ) ) dataset = as.data.frame( sapply( dataset, as.numeric ) ) # Spliting training and testing dataset index = sample( 1:nrow( dataset ), nrow( dataset ) * 0.6, replace = FALSE ) trainset = dataset[ index, ] test = dataset[ -index, ] testset = test %>% select( -class ) # Building a neural network (NN) library( neuralnet ) n = names( trainset ) f = as.formula( paste( "class ~", paste( n[!n %in% "class"], collapse = "+" ) ) ) nn = neuralnet( f, trainset, hidden = 4, linear.output = FALSE, threshold = 0.01 ) plot( nn, rep = "best" )
# Testing the result output nn.results = compute( nn, testset ) results = data.frame( actual = test$class, prediction = round( nn.results$net.result ) ) # Confusion matrix library( caret ) t = table( results ) print( confusionMatrix( t ) )## Confusion Matrix and Statistics ## ## prediction ## actual 0 1 ## 0 79 0 ## 1 79 16 ## ## Accuracy : 0.545977 ## 95% CI : (0.4688867, 0.6214742) ## No Information Rate : 0.908046 ## P-Value [Acc > NIR] : 1 ## ## Kappa : 0.1553398 ## Mcnemar's Test P-Value : <0.0000000000000002 ## ## Sensitivity : 0.5000000 ## Specificity : 1.0000000 ## Pos Pred Value : 1.0000000 ## Neg Pred Value : 0.1684211 ## Prevalence : 0.9080460 ## Detection Rate : 0.4540230 ## Detection Prevalence : 0.4540230 ## Balanced Accuracy : 0.7500000 ## ## 'Positive' Class : 0 ##
Risultati senza PCA
Sembra che abbiamo ottenuto alcuni risultati. In primo luogo, date un’occhiata alla matrice di confusione. Fondamentalmente, la matrice di confusione dice quanto gli esempi sono stati classificati in classi. La diagonale principale mostra gli esempi che sono stati classificati correttamente e diagonale secondaria mostra errata classificazione. In questo primo risultato, il classificatore si mostra molto confuso, perché ha classificato correttamente quasi tutti gli esempi di classe “Saab”, ma ha anche classificato la maggior parte degli esempi di classe “bus” come classe “Saab”. Rafforzando questi risultati, possiamo vedere che il valore di precisione è di circa il 50%, è un risultato davvero negativo per il compito di classificazione. Il classificatore ha essenzialmente una probabilità del 50% di classificare un nuovo esempio in classe “car” e del 50% in classi “bus”. Analogicamente, la rete neurale lancia una moneta per ogni nuovo esempio per scegliere in quale classe classificarla.
Vediamo se PCA può aiutarci
Ora, eseguiamo l’analisi dei componenti principali sul set di dati e otteniamo gli autovalori e gli autovettori. In modo pratico, vedrete che la funzione PCA del pacchetto R fornisce un insieme di autovalori già ordinati in ordine decrescente, significa che il primo componente è quello con la più alta varianza, il secondo componente è l’autovettore con la seconda varianza più alta e così via. Il codice qui sotto mostra come scegliere gli autovettori guardando gli autovalori.
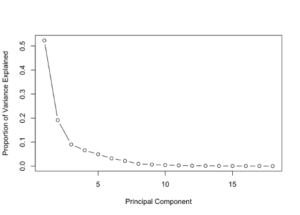
# PCA pca_trainset = trainset %>% select( -class ) pca_testset = testset pca = prcomp( pca_trainset, scale = T ) # variance pr_var = ( pca$sdev )^2 # % of variance prop_varex = pr_var / sum( pr_var ) # Plot plot( prop_varex, xlab = "Principal Component", ylab = "Proportion of Variance Explained", type = "b" )
# Scree Plot plot( cumsum( prop_varex ), xlab = "Principal Component", ylab = "Cumulative Proportion of Variance Explained", type = "b" )
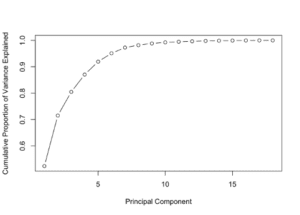
La funzione nativa R “prcomp” dai pacchetti di default stats esegue PCA, restituisce tutti gli autovalori e gli autovettori necessari. Il primo grafico mostra la percentuale di varianza di ogni caratteristica. Potete vedere che il primo componente ha la varianza più alta, un valore intorno al 50% mentre l’ottavo componente è intorno allo 0% della varianza. Quindi indica che dovremmo prendere i primi otto componenti. La seconda figura mostra un’altra prospettiva della varianza, sebbene la somma cumulativa su tutta la varianza, si può vedere che i primi otto autovalori corrispondono a circa il 98% della varianza complessiva. In effetti, è un numero abbastanza buono, significa che c’è solo il 2% delle informazioni perse. Il più grande vantaggio è che ci stiamo muovendo da uno spazio con diciotto caratteristiche ad un altro con solo otto caratteristica perdendo solo il 2% delle informazioni. Questo è il potere della riduzione dimensionale, definitivamente.
Ora che conosciamo il numero delle caratteristiche che comporranno il nuovo spazio, creiamo il nuovo set di dati e poi modelliamo di nuovo la rete neurale e controlliamo se otteniamo nuovi risultati migliori.
# Creating a new dataset train = data.frame( class = trainset$class, pca$x ) t = as.data.frame( predict( pca, newdata = pca_testset ) ) new_trainset = train[, 1:9] new_testset = t[, 1:8] # Build the neural network (NN) library( neuralnet ) n = names( new_trainset ) f = as.formula( paste( "class ~", paste( n[!n %in% "class" ], collapse = "+" ) ) ) nn = neuralnet( f, new_trainset, hidden = 4, linear.output = FALSE, threshold=0.01 ) # Plot the NN plot( nn, rep = "best" )
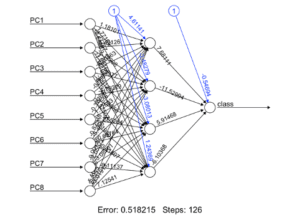
# Test the resulting output nn.results = compute( nn, new_testset ) # Results results = data.frame( actual = test$class, prediction = round( nn.results$net.result ) ) # Confusion Matrix library( caret ) t = table( results ) print( confusionMatrix( t ) )## Confusion Matrix and Statistics ## ## prediction ## actual 0 1 ## 0 76 3 ## 1 1 94 ## ## Accuracy : 0.9770115 ## 95% CI : (0.9421888, 0.9937017) ## No Information Rate : 0.5574713 ## P-Value [Acc > NIR] : < 0.00000000000000022 ## ## Kappa : 0.9535318 ## Mcnemar's Test P-Value : 0.6170751 ## ## Sensitivity : 0.9870130 ## Specificity : 0.9690722 ## Pos Pred Value : 0.9620253 ## Neg Pred Value : 0.9894737 ## Prevalence : 0.4425287 ## Detection Rate : 0.4367816 ## Detection Prevalence : 0.4540230 ## Balanced Accuracy : 0.9780426 ## ## 'Positive' Class : 0 ##
Beh, immagino che ora abbiamo risultati migliori. Esaminiamolo attentamente.
La matrice di confusione mostra risultati veramente buoni questa volta, la rete neurale sta commettendo meno errori di classificazione in entrambe le classi, si può vedere se i valori della diagonale principale e anche il valore di precisione è di circa il 95%. Significa che il classificatore ha il 95% di probabilità di classificare correttamente un nuovo esempio invisibile. Per i problemi di classificazione, non è affatto un cattivo risultato.
Conclusione
La riduzione della dimensionalità gioca un ruolo molto importante nel machine learning, soprattutto quando si lavora con migliaia di funzioni. L’analisi dei componenti principali è uno dei migliori algoritmi di riduzione della dimensionalità, non è difficile capirla e usarla in progetti reali. Questa tecnica, oltre a rendere più facile il lavoro di manipolazione delle funzionalità, aiuta ancora a migliorare i risultati del classificatore, come abbiamo visto in questo post.
Infine, la risposta della domanda iniziale è sì, infatti Principal Component Analysis aiuta a migliorare il risultato di un classificatore.
Cosa viene dopo?
Come ho detto prima ci sono altre tecniche di riduzione della dimensionalità disponibili, come l’Analisi Discriminante Lineare, l’Analisi Fattoriale, l’Isomappa e le sue variazioni. L’ideia è esplorare vantaggi e svantaggi di ciascuno e controllare i suoi risultati individualmente e combinati. Sarebbe LDA combinato con PCA migliorare il risultato classificatori? Bene, cerchiamo di indagare nei prossimi post.
Il codice completo è disponibile sul mio repository hub git così come il set di dati. ( https://github.com/Meigarom/machine_learning )
Grazie per il tuo tempo leggendo questo post. Ho apprezzato molto, i feedback sono sempre i benvenuti.
A presto.
Articoli su Towards Data Science: https://medium.com/@meigaromlopes
Profilo Linkedin: https://www.linkedin.com/in/meigarom/
Share: