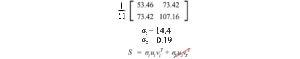Apprendimento automatico – Decomposizione del valore singolare (SVD) e analisi dei componenti principali (PCA)
Articolo originale in lingua inglese di Jonathan Hui

Nell’apprendimento automatico (ML), alcuni dei più importanti concetti di algebra lineare sono la scomposizione del valore singolare (SVD) e l’analisi dei componenti principali (PCA). Con tutti i dati grezzi raccolti, come possiamo scoprire le strutture? Ad esempio, con i tassi di interesse degli ultimi 6 giorni, possiamo capire la sua composizione per individuare le tendenze?

Questo diventa ancora più difficile per i dati grezzi ad alta dimensione. È come trovare un ago in un pagliaio. SVD ci permette di estrarre e districare informazioni. In questo articolo, descriveremo in dettaglio SVD e PCA. Presumiamo che tu abbia una conoscenza di base di algebra lineare, inclusi i rank e gli autovettori. Se si verificano difficoltà nella lettura di questo articolo, vi suggerisco rinfrescare quei concetti prima. Alla fine dell’articolo, risponderemo ad alcune domande nell’esempio del tasso di interesse sopra. Questo articolo contiene anche sezioni opzionali. Sentitevi liberi di saltare in base al vostro livello di interesse.
Idee sbagliate (opzionale per i principianti)
Mi rendo conto di alcune domande comuni che i non principianti possono chiedere. Vorrei affrontare l’elefante nella stanza prima. È PCA riduzione della dimensione? PCA riduce la dimensione, ma è molto di più. Mi piace la descrizione Wiki (ma se non si conosce PCA, questo è solo incomprensibile):
L’analisi delle componenti principali (PCA) è una procedura statistica che utilizza una trasformazione ortogonale per convertire un insieme di osservazioni di variabili eventualmente correlate (entità ciascuna delle quali assume vari valori numerici) in un insieme di valori di variabili linearmente non correlate chiamate componenti principali.
Da una prospettiva semplificata, il PCA trasforma i dati linearmente in nuovi beni che non sono correlati con a vicenda. Per ML, il posizionamento di PCA come funzione di estrazione può consentirci di esplorare il suo potenziale meglio della riduzione delle dimensioni.
Qual è la differenza tra SVD e PCA? SVD ti dà l’intero nove metri di diagonalizzazione di una matrice in matrici speciali che sono facili da manipolare e da analizzare. Stabilisce le basi per districare i dati in componenti indipendenti. PCA salta componenti meno significativi. Ovviamente, possiamo usare SVD per trovare PCA troncando i vettori di base meno importanti nella matrice SVD originale.
Diagonalizzazione della matrice
Nell’articolo sugli autovalori e autovettori, descriviamo un metodo per scomporre una matrice quadrata n × n A in
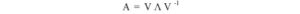
Per esempio,
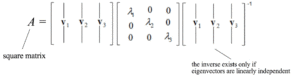
Una matrice può essere diagonalizzata se A è una matrice quadrata e A ha n autovettori linearmente indipendenti. Ora, è il momento di sviluppare una soluzione per tutte le matrici che utilizzano SVD.
Vettori singolari e valori singolari
La matrice AAᵀ e AᵀA sono veramente speciali in algebra lineare. Considerare qualsiasi matrice A m × n, possiamo moltiplicarlo con Aᵀ per formare AAᵀ e AᵀA separatamente. Queste matrici sono:
- simmetriche,
- quadrate,
- almeno semidefinito positivo (gli autovalori sono zero o positivi),
- entrambe le matrici hanno gli stessi autovalori positivi, e
- entrambi hanno lo stesso grado r di A.
Inoltre, le matrici di covarianza che usiamo spesso in ML sono in questa forma. Dal momento che sono simmetrici, possiamo scegliere i suoi autovettori per essere ortonormali (perpendicolari tra loro con lunghezza unitaria) – questa è una proprietà fondamentale per le matrici simmetriche.

Introduciamo alcuni termini usati frequentemente in SVD. Chiamiamo gli autovettori di AAᵀ come uᵢ e AᵀA come vᵢ qui e chiamiamo questi insiemi di autovettori u e v i singoli vettori di A. Entrambe le matrici hanno gli stessi autovalori positivi. Le radici quadrate di questi autovalori sono chiamate valori singolari.
Non troppe spiegazioni finora, ma mettiamo tutto insieme prima e le spiegazioni verranno dopo. Noi concatenare vettori uᵢ in U e vᵢ in V per formare matrici ortogonali.

Poiché questi vettori sono ortonormali, è facile dimostrare che U e V obbediscono
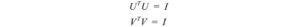
SVD
Iniziamo prima con la parte difficile. SVD afferma che qualsiasi matrice A può essere fattorizzata come:
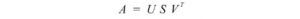
dove U e V sono matrici ortogonali con autovettori ortonormali scelti rispettivamente tra AAᵀ e AᵀA. S è una matrice diagonale con r elementi uguali alla radice degli autovalori positivi di of AAᵀ o Aᵀ A (entrambe le matrici hanno comunque gli stessi autovalori positivi). Gli elementi diagonali sono composti da valori singolari.

i.e. una matrice m × n può essere fattorizzata come:
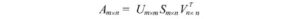
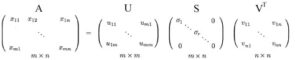
Possiamo organizzare autovettori in ordini diversi per produrre U e V. Per standardizzare la soluzione, ordiniamo agli autovettori in modo tale che i vettori con autovalori più elevati vengano prima di quelli con valori più piccoli.
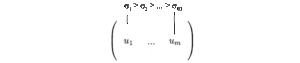
Confrontando la composizione degli autovalori, SVD funziona su matrici non quadrate. U e V sono invertibili per qualsiasi matrice in SVD e sono ortonormali che lo amiamo. Senza prove qui, vi diciamo anche che i valori singolari sono più stabili numericamente rispetto agli autovalori.
Esempio (Fonte dell’esempio)
Prima di andare troppo lontano, mostriamolo con un semplice esempio. Questo renderà le cose molto facili da capire.
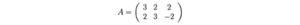
Calcoliamo:

Queste matrici sono almeno semidefinite positive (tutti gli autovalori sono positivi o nulli). Come mostrato, condividono gli stessi autovalori positivi (25 e 9). La figura sotto mostra anche i loro autovettori corrispondenti.

I valori singolari sono la radice quadrata degli autovalori positivi, cioè 5 e 3. Pertanto, la composizione SVD è
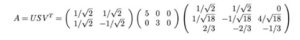
Prova (facoltativa)
Per provare SVD, vogliamo risolvere U, S e V con:
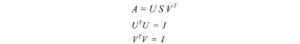
Abbiamo 3 incognite. Speriamo, possiamo risolverli con le 3 equazioni sopra. Il transpose di A è
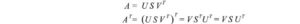
Sapendo
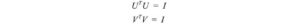
Computiamo AᵀA,
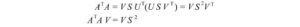
L’ultima equazione è equilvante alla definizione autovettore per la matrice (AᵀA). Abbiamo appena messo tutti gli autovettori in una matrice.

con VS² equivale a

V contiene tutti gli autovettori vᵢ di AᵀA e S contiene le radici quadrate di tutti gli autovalori of AᵀA. Possiamo ripetere lo stesso processo per AAᵀ e tornare indietro con un’equazione similare.
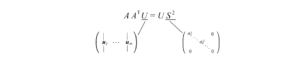
Adesso, risolviamo solo U, V e S per
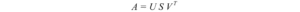
e dimostriamo il teorema.
Riepilogo
Il seguente è un riassunto di SVD.

dove
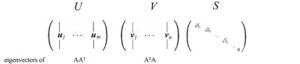
Riformulare la SVD
Poiché la matrice V è ortogonale, VᵀV equivale a I. Possiamo riscrivere l’equazione SVD come:
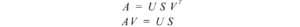
Questa equazione stabilisce un importante relazione tra uᵢ e vᵢ. Richiama
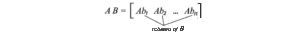
Applicare AV = US,
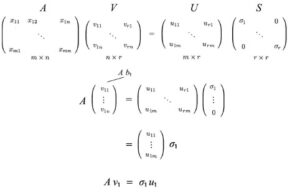
Questo può essere generalizzato come

Richiama,
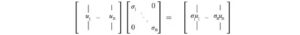
e
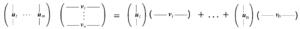
La decomposizione SVD può essere riconosciuta come una serie di prodotti esterni di uᵢ e vᵢ.

Questa formula di SVD è la chiave per capire i componenti di A. Fornisce un modo importante per scomporre un array m n di dati impigliati in componenti r. Poiché uᵢ e vᵢ sono vettori unitari, possiamo anche ignorare i termini (σᵢuᵢvᵢᵀ) con un valore singolare σᵢ. (Torneremo su questo più avanti.)
Prima riutilizziamo l’esempio e mostriamo come funziona.
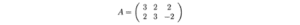
La matrice A di cui sopra può essere scomposta come
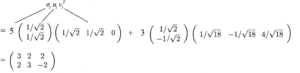
Spazio colonna, spazio riga, nullspace sinistro e nullspace (opzionale-per utenti avanzati)
Successivamente, daremo un’occhiata a ciò che è composto da U & V. Diciamo che A è una matrice m × n di rango r. AᵀA sarà una matrice n simmetrica di n × n. Tutte le matrici simmetriche possono scegliere n autovettori ortonormali vⱼ. A causa del fatto che Avᵢ = σᵢuᵢ e vⱼ sono autovettori ortonormali di AᵀA, possiamo calcolare il valore di uᵢᵀuⱼ come
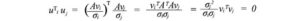
È uguale a zero. i.e. uᵢ e uⱼ sono ortogonali a vicenda. Come mostrato in precedenza, sono anche autovettori di AAᵀ.
Da Avᵢ = σuᵢ, possiamo definire che uᵢ è un vettore di colonna di A.

Perché A ha un rango di r, possiamo scegliere questi vettori r, uᵢ come ortonormali. Quindi quali sono i rimanenti autovettori ortogonali m – r per AAᵀ? Poiché lo spazio nullo lasciato da A è ortogonale allo spazio della colonna, è molto naturale selezionarli come autovettore restante. (Lo spazio nullo rimasto N(Aᵀ) è lo space span di x in Aᵀx=0.) Un argomento similar funzionerà per gli autovettori di AᵀA. Pertanto,

Per tornare alla precedente equazione SVD da
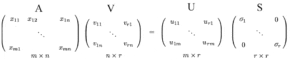
Semplicemente rimettiamo gli autovettori tra gli spazi nulli rimasti.
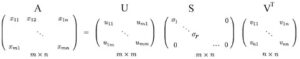
Moore-Penrose Pseudoinverso
Per un sistema di equazioni lineari, possiamo calcolare l’inverso di una matrice quadrata A per risolvere x.
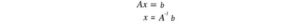
Ma non tutte le matrici sono invertibili. Inoltre, in ML, sarà improbabile trovare una soluzione esatta con la presenza di rumore nei dati. Il nostro obiettivo è trovare il modello più adatto ai dati. Per trovare la soluzione più adatta, calcoliamo uno pseudoinverso
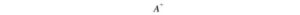
che minimizza il minimo errore quadrato sotto.
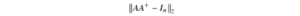
E la soluzione per x può essere stimata come,
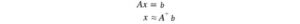
In un problema di regressione lineare, x è il nostro modello lineare, A contiene i dati di allenamento e b contiene le etichette corrispondenti. Possiamo risolvere x per

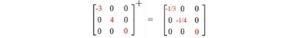
Ecco qui un esempio.

Varianza & covarianza
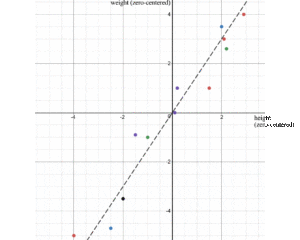
In ML, identifichiamo modelli e relazioni. Come identifichiamo la correlazione delle proprietà nei dati? Iniziamo la discussione con un esempio. Campioniamo l’altezza e il peso di 12 persone e calcoliamo i loro mezzi. Concentriamo i valori originali sottraendoli con la loro media. Per esempio, la matrice A sotto tiene l’altezza e il peso zero-centrati regolati.
Mentre tracciamo i punti dati, possiamo riconoscere che altezza e peso sono positivamente correlati. Ma come possiamo quantificare tale relazione?
Primo, come varia una proprietà? Probabilmente impariamo la varianza dal liceo. Presentiamo suo cugino. La varianza del campione è definita come:
Nota, è diviso per n-1 invece di n nella varianza. Con una dimensione limitata dei campioni, la media del campione è distorta e correlata con i campioni. La distanza quadrata media da questa media sarà più piccola di quella dalla popolazione generale. La covarianza del campione S², diviso per n-1, compensa il valore minore e può essere dimostrata una stima imparziale della varianza σ². ((La prova non è molto importante quindi mi limiterò a fornire un link per la prova qui.)
Matrici di covarianza
La varianza misura come una variabile varia tra di sé mentre la covarianza è tra due variabili (a e b).
Possiamo tenere tutte queste possibili combinazioni di covarianza in una matrice chiamata matrice di covarianza Σ.
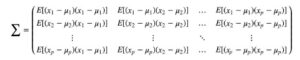
Possiamo riscriverlo in una semplice matrice.
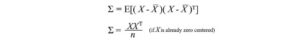
Gli elementi diagonali mantengono le varianze delle singole variabili (come l’altezza) e gli elementi non diagonali mantengono la covarianza tra due variabili. Ora calcoliamo la covarianza del campione.

Gli elementi diagonali mantengono le varianze delle singole variabili (come l’altezza) e gli elementi non diagonali mantengono la covarianza tra due variabili. Ora calcoliamo la covarianza del campione.
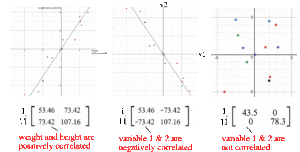
Matrice di covarianza e SVD
Possiamo usare SVD per decomporre la matrice di covarianza del campione. Dato che σ₂ è relativamente piccola rispetto a σ₁, possiamo anche ignorare il termine σ₂. Quando formiamo un modello ML, possiamo eseguire una regressione lineare sul peso e sull’altezza per formare una nuova proprietà piuttosto che trattarle come due proprietà separate e correlate (dove i dati impigliati di solito rendono l’allenamento del modello più difficile).
u₁ ha un’importanza significativa. È il componente principale di S.
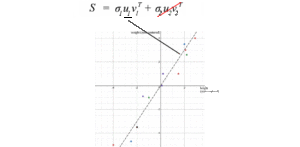
Ci sono alcune proprietà circa una matrice di covarianza del campione nell’ambito del contesto di SVD:
- La varianza totale dei dati equivale alla traccia della matrice di covarianza del campione S che è uguale alla somma dei quadrati dei valori singolari di S. Dotato di questo, possiamo calcolare il rapporto di varianza perso se scendiamo più piccoli termini σᵢ. Questo riflette la quantità di informazioni perse se li eliminiamo.
- Il primo autovettore u₁ diS indica la direzione più importante dei dati. Nel nostro esempio, quantifica il rapporto tipico tra peso e altezza.
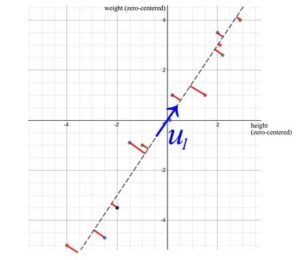
- L’errore, calcolato come la somma della distanza quadrata perpendicolare dai punti del campione a u , è il minimo quando si usa SVD.
Proprietà
Le matrici di covarianza non sono solo simmetriche ma sono anche semidefinite positive. Poiché la varianza è positiva o zero, uᵀVu otto è sempre maggiore o uguale a zero. Con il test di energia, V è semidefinito positivo.
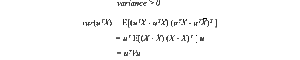
Pertanto,
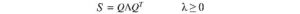
Spesso, dopo qualche trasformazione lineare A, ogliamo conoscere la covarianza dei dati trasformati. Questo può essere calcolato con la matrice di trasformazione A e la covarianza dei dati originali.
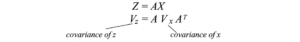
Matrice di correlazione
Una matrice di correlazione è una versione in scala della matrice di covarianza. Una matrice di correlazione standardizza (scala) le variabili per avere una deviazione standard di 1.

Una matrice di correlazione è una versione in scala della matrice di covarianza. Una matrice di correlazione standardizza (scala) le variabili per avere una deviazione standard di 1.
Visualizzazione
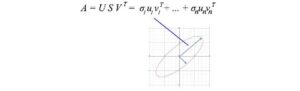
Finora abbiamo molte equazioni. Visualizziamo cosa fa SVD e sviluppiamo gradualmente l’insight. SVD scompone una matrice A in USVᵀ. L’applicazione di A a un vettore x (Ax) può essere visualizzata come l’esecuzione di una rotazione (Vᵀ), un ridimensionamento (S) e un’altra rotazione (U) su x.
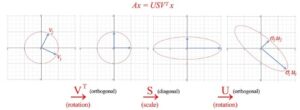
Come mostrato sopra, l’autovettore vᵢ di V si trasforma in:
O nella forma matrice completa
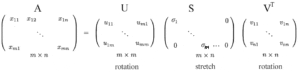
Visione di SVD
Come descritto prima, il SVD può essere formulato come

Poiché uᵢ e vᵢ hanno lunghezza unitaria, il fattore più importante per determinare il significato di ciascun termine è il valore singolare σᵢ. Abbiamo volutamente ordinare σᵢ nell’ordine discendente. Se gli autovalori diventano troppo piccoli, possiamo ignorare i restanti termini (+ σᵢuᵢvᵢᵀ + …).
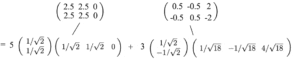
Questa compilazione ha alcune implicazioni interessanti. Ad esempio, abbiamo una matrice contiene il rendimento dei rendimenti azionari negoziati da diversi investitori.

Come gestore di fondi, quali informazioni possiamo ricavarne? Trovare modelli e strutture sarà il primo passo. Forse, possiamo identificare la combinazione di azioni e investitori che hanno i maggiori rendimenti. SVD decompone una matrice n × n in r componenti con il valore singolare σᵢ dimostrando il suo significativo. Considera questo come un modo per estrarre proprietà impigliate e correlate in meno direzioni principali senza correlazioni.
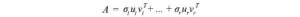
Se i dati sono altamente correlati, dovremmo aspettarci che molti valori σᵢ siano piccoli e possano essere ignorati.
Nel nostro esempio precedente, peso e altezza sono strettamente correlati. Se abbiamo una matrice contenente il peso e l’altezza di 1000 persone, il primo componente nella decomposizione SVD dominerà. Il vettore u₁ infatti dimostra il rapporto tra peso e altezza tra queste 1000 persone come abbiamo discusso prima.

Analisi dei componenti principali (PCA)
Tecnicamente, SVD estrae i dati nelle direzioni con le più alte varianze rispettivamente. Il PCA è un modello lineare nella mappatura delle caratteristiche di input m-dimensionale ai fattori latenti k-dimensionali (k componenti principali). Se ignoriamo i termini meno significativi, rimuoviamo i componenti che ci interessano di meno ma manteniamo le direzioni principali con le più alte varianze (informazioni più grandi).

Considerare i punti di dati tridimensionali che vengono visualizzati come punti blu sotto. Può essere facilmente approssimato da un piano.
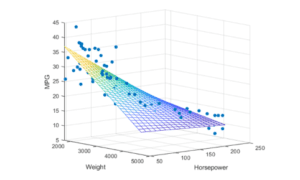
Si può rapidamente rendersi conto che possiamo usare SVD per trovare la matrice W. Si considerino i punti di dati sotto che si trovano su uno spazio 2-D.
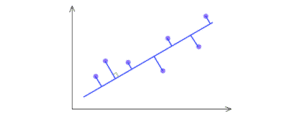
SVD seleziona una proiezione che massimizza la varianza della loro uscita. Quindi, PCA selezionerà la linea blu sopra la linea verde se ha una più alta varianza.
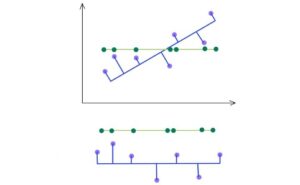
Come indicato di seguito, manteniamo gli autovettori che hanno il valore superiore kth più alto singolare.
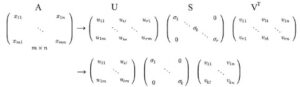
Tasso di interesse
Illustriamo il concetto più in profondità ripercorrendo un esempio qui con i dati sui tassi di interesse provenienti dal Dipartimento del Tesoro degli Stati Uniti. I punti base per 9 diversi tassi di interesse (da 3 mesi, 6 mesi, … a 20 anni) su 6 giorni lavorativi consecutivi sono raccolti con A memorizzato la differenza dalla data precedente. A ha anche i suoi elementi sottratti dalla sua media in questo periodo già. i.e. è zero-centrato (attraverso la sua riga).
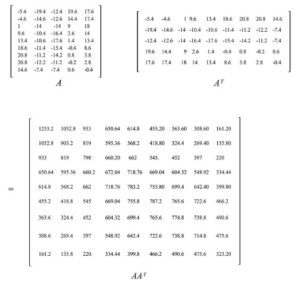
La matrice di covarianza del campione è uguale a S = AAᵀ/(5–1).
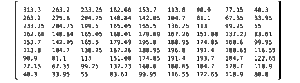
Ora abbiamo la matrice di covarianza S che vogliamo fattorizzare. La decomposizione SVD è
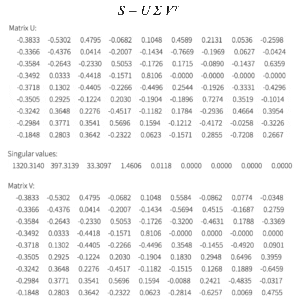
Dalla decomposizione SVD, ci rendiamo conto che possiamo concentrarci sui primi tre componenti principali.
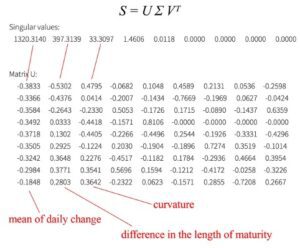
Come illustrato, la prima componente principale è correlata a una media ponderata della variazione giornaliera per tutte le scadenze. La seconda componente principale regola la variazione giornaliera sensibile alla durata del titolo. (La terza componente principale è probabilmente la curvatura – un derivato di secondo grado.)
Comprendiamo bene il rapporto tra variazione dei tassi di interesse e maturità nella nostra vita quotidiana. Così le componenti principali riconfermano quello che crediamo come si comportano i tassi di interesse. Ma quando ci vengono presentati dati grezzi sconosciuti, PCA è molto utile per estrarre i componenti principali dei dati per trovare la struttura sottostante informazioni. Questo può rispondere ad alcune domande su come trovare un ago in un pagliaio.
Suggerimenti
Ridimensiona le funzionalità prima di eseguire SVD.
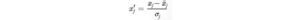
Diciamo, vogliamo mantenere la varianza del 99%, possiamo scegliere k tale che
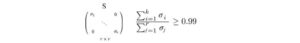
Articoli su Towards Data Science: https://jonathan-hui.medium.com
Profilo Linkedin: https://www.linkedin.com/in/thejonathanhui/
Share: