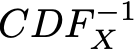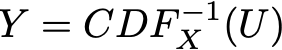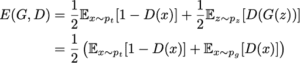Comprendere le reti avversarie generative (GAN)
Introduzione
Yann LeCun l’ha definita “l’idea più interessante degli ultimi 10 anni nel campo del Machine Learning”. Naturalmente, un tale complimento proveniente da un ricercatore così importante nel campo dell’apprendimento profondo è sempre una grande pubblicità per l’argomento di cui stiamo parlando! E, in effetti, le Generative Adversarial Networks (in breve GAN) hanno avuto un enorme successo da quando sono state introdotte nel 2014 da Ian J. Goodfellow e coautori nell’articolo Generative Adversarial Nets.
Cosa sono dunque le Reti Generative Adversariali? Cosa le rende così “interessanti”? In questo post, vedremo che l’adversarial training è un’idea illuminante, bella per la sua semplicità, che rappresenta un vero progresso concettuale per il Machine Learning e più in particolare per i modelli generativi (allo stesso modo in cui la backpropagation è un trucco semplice ma davvero intelligente che ha reso l’idea di base delle reti neurali così popolare ed efficiente).
Prima di entrare nei dettagli, diamo una rapida panoramica di ciò che le GAN sono in grado di fare. Le reti avversarie generative appartengono all’insieme dei modelli generativi di cui abbiamo anche un corso specifico presente sulla nostra piattaforma. Ciò significa che sono in grado di produrre/generare (vedremo come) nuovi contenuti. Per illustrare questa nozione di “modelli generativi”, possiamo dare un’occhiata ad alcuni noti esempi di risultati ottenuti con le GAN.
Illustrazione delle capacità delle GAN di Ian Goodfellow e coautori. Questi sono campioni generati da reti avversarie generative dopo l’addestramento su due set di dati: MNIST e TFD. Per entrambi, la colonna più a destra contiene i dati veri più vicini ai campioni generati. Questo dimostra che i dati prodotti sono realmente generati e non solo memorizzati dalla rete. (fonte: documento “Generative Adversarial Nets”)
Naturalmente, questa capacità di generare nuovi contenuti fa sembrare i GAN un po’ “magici”, almeno a prima vista. Nelle parti che seguono, supereremo l’apparente magia delle GAN per immergerci nelle idee, nella matematica e nella modellazione alla base di questi modelli. Non solo discuteremo le nozioni fondamentali su cui si basano le Reti Generative Adversariali ma, soprattutto, costruiremo passo dopo passo e partendo dall’inizio il ragionamento che porta a queste idee.
Senza ulteriori indugi, riscopriamo insieme le GAN!
Nota: anche se abbiamo cercato di rendere questo articolo il più autonomo possibile, è comunque necessaria una conoscenza di base del Machine Learning. Ciononostante, la maggior parte delle nozioni verrà mantenuta quando necessario e, in caso contrario, verranno forniti alcuni riferimenti. Abbiamo cercato di rendere questo articolo il più scorrevole possibile. Non esitate a segnalare nella sezione dei commenti ciò che avreste voluto leggere di più (per eventuali altri articoli sull’argomento).
Schema
Nella prima sezione che segue discuteremo il processo di generazione di variabili casuali a partire da una data distribuzione
. Nella sezione 2 mostreremo, attraverso un esempio, che i problemi che le GAN cercano di affrontare possono essere espressi come problemi di generazione di variabili casuali. Nella sezione 3 discuteremo le reti generative basate sul matching e mostreremo come rispondono ai problemi descritti nella sezione 2. Infine, nella sezione 4 introdurremo le GAN. Infine, nella sezione 4 presenteremo le GAN. In particolare, presenteremo l’architettura generale con la sua funzione di perdita e faremo il collegamento con tutte le parti precedenti.
– Questo articolo è stato completato con il seguente cheatsheet:
https://drive.google.com/drive/folders/1lHtjHQ8K7aemRQAnYMylrrwZp6Bsqqrb
– Questo articolo è stato in parte illustrato con il seguente breve video:
Generazione di variabili casuali
In questa sezione, discutiamo il processo di generazione delle variabili casuali: ricordiamo alcuni metodi esistenti e in particolare il metodo della trasformata inversa, che permette di generare variabili casuali complesse da semplici variabili casuali uniformi. Anche se tutto questo potrebbe sembrare un po’ lontano dal nostro argomento, le GAN, vedremo nella prossima sezione il profondo legame che esiste con i modelli generativi.
Le variabili casuali uniformi possono essere generate in modo pseudocasuale
I computer sono fondamentalmente deterministici. Quindi, in teoria, è impossibile generare numeri che siano davvero casuali (anche se potremmo dire che la domanda “che cos’è davvero la casualità?” è difficile). Tuttavia, è possibile definire algoritmi che generano sequenze di numeri le cui proprietà sono molto vicine a quelle delle sequenze di numeri casuali teorici. In particolare, un computer è in grado, utilizzando un generatore di numeri pseudorandom, di generare una sequenza di numeri che segue approssimativamente una distribuzione casuale uniforme tra 0 e 1. Il caso uniforme è un caso molto semplice su cui si possono costruire variabili casuali più complesse in diversi modi.
Variabili casuali espresse come risultato di un’operazione o di un processo
Esistono diverse tecniche che mirano a generare variabili casuali più complesse. Tra queste troviamo, ad esempio, il metodo della trasformazione inversa, il campionamento per scarto, l’algoritmo di Metropolis-Hasting e altri ancora.
. Tutti questi metodi si basano su diversi trucchi matematici che consistono principalmente nel rappresentare la variabile casuale che vogliamo generare come il risultato di un’operazione (su variabili casuali più semplici) o di un processo.
Il campionamento a rifiuto esprime la variabile casuale come il risultato di un processo che consiste nel campionare non dalla distribuzione complessa ma da una distribuzione semplice ben nota e nell’accettare o rifiutare il valore campionato a seconda di alcune condizioni. Ripetendo questo processo finché il valore campionato non viene accettato, possiamo dimostrare che con la giusta condizione di accettazione il valore che verrà effettivamente campionato seguirà la giusta distribuzione.
Nell’algoritmo di Metropolis-Hasting, l’idea è di trovare una Catena di Markov (MC) tale che la distribuzione stazionaria di questa MC corrisponda alla distribuzione da cui vogliamo campionare la nostra variabile casuale. Una volta trovata questa MC, possiamo simulare una traiettoria abbastanza lunga su questa MC per considerare che abbiamo raggiunto uno stato stazionario e quindi l’ultimo valore ottenuto in questo modo può essere considerato come estratto dalla distribuzione di interesse.
Non ci addentreremo ulteriormente nei dettagli del campionamento per scarto e di Metropolis-Hasting perché non sono questi i metodi che ci porteranno alla nozione di GAN (tuttavia, il lettore interessato può fare riferimento agli articoli di Wikipedia e ai relativi link). Tuttavia, concentriamoci un po’ di più sul metodo della trasformazione inversa.
Il metodo della trasformazione inversa
L’idea del metodo della trasformazione inversa è semplicemente quella di rappresentare la nostra variabile casuale complessa – in questo articolo “complessa” va sempre inteso nel senso di “non semplice” e non in senso matematico – come il risultato di una funzione applicata a una variabile casuale uniforme che sappiamo come generare.
Di seguito consideriamo un esempio monodimensionale. Sia X una variabile casuale complessa che vogliamo campionare e U una variabile casuale uniforme su [0,1] che sappiamo campionare. Ricordiamo che una variabile casuale è completamente definita dalla sua funzione di distribuzione cumulativa (CDF). La CDF di una variabile casuale è una funzione che va dal dominio di definizione della variabile casuale all’intervallo [0,1] ed è definita, in una dimensione, in modo tale che
Nel caso particolare della nostra variabile casuale uniforme U, si ha
Per semplicità, si supporrà che la funzione CDF_X sia invertibile e che la sua inversa sia indicata come
(il metodo può essere facilmente esteso al caso non invertibile utilizzando l’inversa generalizzata della funzione, ma non è questo il punto principale su cui vogliamo concentrarci). Quindi, se definiamo
abbiamo
Come si può notare, Y e X hanno la stessa CDF e quindi definiscono la stessa variabile casuale. Quindi, definendo Y come sopra (come funzione di una variabile casuale uniforme) siamo riusciti a definire una variabile casuale con la distribuzione desiderata.
In sintesi, il metodo della trasformazione inversa è un modo per generare una variabile casuale che segue una determinata distribuzione facendo passare una variabile casuale uniforme attraverso una “funzione di trasformazione” ben progettata (CDF inversa). Questa nozione di “metodo della trasformazione inversa” può, infatti, essere estesa alla nozione di “metodo della trasformazione” che consiste, più in generale, nel generare variabili casuali in funzione di alcune variabili casuali più semplici (non necessariamente uniformi e quindi la funzione di trasformazione non è più la CDF inversa). Concettualmente, lo scopo della “funzione di trasformazione” è quello di deformare/rimodellare la distribuzione di probabilità iniziale: la funzione di trasformazione prende da dove la distribuzione iniziale è troppo alta rispetto alla distribuzione desiderata e la mette dove è troppo bassa.
Modelli generativi
Cerchiamo di generare variabili casuali molto complesse…
Supponiamo di essere interessati a generare immagini quadrate in bianco e nero di cani di dimensioni n per n pixel. Possiamo rimodellare ogni dato come un vettore di N=nxn dimensioni (impilando le colonne una sull’altra) in modo che l’immagine di un cane possa essere rappresentata da un vettore. Tuttavia, ciò non significa che tutti i vettori rappresentino un cane una volta che sia stato rimodellato in un quadrato! Quindi, possiamo dire che gli N vettori dimensionali che danno effettivamente l’immagine di un cane sono distribuiti secondo una distribuzione di probabilità molto specifica sull’intero spazio vettoriale N dimensionale (è molto probabile che alcuni punti di questo spazio rappresentino dei cani, mentre è altamente improbabile per altri). Nello stesso spirito, esistono, su questo spazio vettoriale a N dimensioni, distribuzioni di probabilità per immagini di gatti, uccelli e così via.
Quindi, il problema di generare una nuova immagine di cane è equivalente al problema di generare un nuovo vettore che segua la “distribuzione di probabilità del cane” sullo spazio vettoriale a N dimensioni. Siamo quindi di fronte a un problema di generazione di una variabile casuale rispetto a una specifica distribuzione di probabilità.
A questo punto, possiamo menzionare due cose importanti. Innanzitutto, la “distribuzione di probabilità del cane” di cui abbiamo parlato è una distribuzione molto complessa su uno spazio molto ampio. In secondo luogo, anche se possiamo ipotizzare l’esistenza di tale distribuzione di fondo (esistono effettivamente immagini che assomigliano a un cane e altre che non lo assomigliano), ovviamente non sappiamo come esprimere esplicitamente questa distribuzione. Entrambi i punti precedenti rendono il processo di generazione di variabili casuali da questa distribuzione piuttosto difficile. Cerchiamo quindi di affrontare questi due problemi nel seguito.
… quindi usiamo il metodo della trasformazione con una rete neurale come funzione!
Il primo problema che abbiamo quando cerchiamo di generare la nostra nuova immagine di cane è che la “distribuzione di probabilità del cane” sullo spazio vettoriale N dimensionale è molto complessa e non sappiamo come generare direttamente variabili casuali complesse. Tuttavia, poiché sappiamo abbastanza bene come generare N variabili casuali uniformi non correlate, possiamo utilizzare il metodo della trasformazione. Per farlo, dobbiamo esprimere la nostra variabile casuale N dimensionale come il risultato di una funzione molto complessa applicata a una semplice variabile casuale N dimensionale!
A questo punto, possiamo sottolineare il fatto che trovare la funzione di trasformazione non è così semplice come prendere l’inversa in forma chiusa della funzione di distribuzione cumulativa (che ovviamente non conosciamo), come abbiamo fatto quando abbiamo descritto il metodo della trasformazione inversa. La funzione di trasformazione non può essere espressa esplicitamente e, quindi, dobbiamo impararla dai dati.
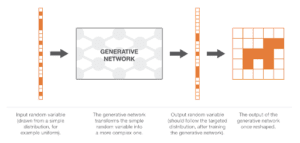
Come spesso accade in questi casi, una funzione molto complessa implica naturalmente la modellazione di una rete neurale. L’idea è quindi quella di modellare la funzione di trasformazione con una rete neurale che prende in ingresso una semplice variabile casuale uniforme a N dimensioni e che restituisce in uscita un’altra variabile casuale a N dimensioni che dovrebbe seguire, dopo l’addestramento, la giusta “distribuzione di probabilità canina”. Una volta progettata l’architettura della rete, è necessario addestrarla. Nelle prossime due sezioni discuteremo due modi per addestrare queste reti generative, compresa l’idea dell’addestramento avversario alla base delle GAN!
Illustrazione della nozione di modelli generativi che utilizzano le reti neurali. Ovviamente, le dimensionalità di cui si parla sono molto più elevate di quelle rappresentate qui.
Reti di corrispondenza generative
Disclaimer: la denominazione di “reti generative di corrispondenza” non è standard. Tuttavia, in letteratura si possono trovare, ad esempio, “Reti di corrispondenza di momenti generativi” o anche “Reti di corrispondenza di caratteristiche generative”. In questa sede vogliamo solo utilizzare una denominazione un po’ più generale per ciò che descriviamo qui di seguito.
Addestramento dei modelli generativi
Finora abbiamo dimostrato che il nostro problema di generare una nuova immagine di cane può essere riformulato in un problema di generazione di un vettore casuale nello spazio vettoriale N-dimensionale che segue la “distribuzione di probabilità del cane” e abbiamo suggerito di utilizzare un metodo di trasformazione, con una rete neurale per modellare la funzione di trasformazione
Ora, dobbiamo ancora addestrare (ottimizzare) la rete per esprimere la giusta funzione di trasformazione. A questo scopo, possiamo proporre due diversi metodi di addestramento: uno diretto e uno indiretto. Il metodo di addestramento diretto consiste nel confrontare le distribuzioni di probabilità vere e quelle generate e nel retropropagare la differenza (l’errore) attraverso la rete. Questa è l’idea alla base delle reti di corrispondenza generativa (GMN). Nel metodo di addestramento indiretto, non si confrontano direttamente le distribuzioni vere e generate. Invece, addestriamo la rete generativa facendo passare queste due distribuzioni attraverso un compito a valle scelto in modo tale che il processo di ottimizzazione della rete generativa rispetto al compito a valle imponga che la distribuzione generata sia vicina alla distribuzione vera. Quest’ultima idea è alla base delle reti generative avversarie (GAN), che presenteremo nella prossima sezione. Per ora, però, iniziamo con il metodo diretto e le GMN.
Confronto tra due distribuzioni di probabilità basate su campioni
Come abbiamo detto, l’idea delle GMN è quella di addestrare la rete generativa confrontando direttamente la distribuzione generata con quella vera. Tuttavia, non sappiamo come esprimere esplicitamente la vera “distribuzione di probabilità del cane” e possiamo anche dire che la distribuzione generata è troppo complessa per essere espressa esplicitamente. Quindi, non è possibile fare confronti basati su espressioni esplicite. Tuttavia, se disponiamo di un modo per confrontare le distribuzioni di probabilità basate su campioni, possiamo utilizzarlo per addestrare la rete. Infatti, abbiamo un campione di dati veri e possiamo, a ogni iterazione del processo di addestramento, produrre un campione di dati generati.
Sebbene, in teoria, si possa utilizzare qualsiasi distanza (o misura di somiglianza) in grado di confrontare efficacemente due distribuzioni basate su campioni, possiamo citare in particolare l’approccio della Maximum Mean Discrepancy (MMD). La MMD definisce una distanza tra due distribuzioni di probabilità che può essere calcolata (stimata) sulla base di campioni di queste distribuzioni. Sebbene non sia del tutto fuori dallo scopo di questo articolo, abbiamo deciso di non dedicare molto tempo alla descrizione della MMD. Tuttavia, abbiamo in progetto di pubblicare presto un articolo che conterrà maggiori dettagli al riguardo. Il lettore che volesse saperne di più sulla MMD può fare riferimento a queste diapositive, a questo articolo o a questo articolo.
Retropropagazione dell’errore di corrispondenza della distribuzione
Una volta definito un modo per confrontare due distribuzioni sulla base di campioni, possiamo definire il processo di addestramento della rete generativa in GMN. Data in ingresso una variabile casuale con distribuzione di probabilità uniforme, vogliamo che la distribuzione di probabilità dell’uscita generata sia la “distribuzione di probabilità del cane”. L’idea delle GMN consiste quindi nell’ottimizzare la rete ripetendo i seguenti passaggi:
– generare alcuni input uniformi
– far passare questi input attraverso la rete e raccogliere gli output generati
– confrontare la vera “distribuzione di probabilità del cane” e quella generata sulla base dei campioni disponibili (ad esempio, calcolare la distanza MMD tra il campione di immagini di cani vere e il campione di immagini generate)
– utilizzare la retropropagazione per effettuare un passo di discesa del gradiente per abbassare la distanza (per esempio MMD) tra le distribuzioni vere e quelle generate.
Come scritto sopra, quando si seguono questi passaggi si applica una discesa del gradiente sulla rete con una funzione di perdita che è la distanza tra le distribuzioni vere e quelle generate all’iterazione corrente.
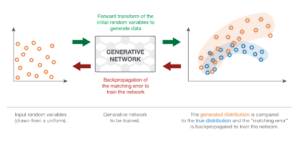
Le reti di corrispondenza generative prendono semplici input casuali, generano nuovi dati, confrontano direttamente la distribuzione dei dati generati con la distribuzione dei dati veri e retropropagano l’errore di corrispondenza per addestrare la rete.
Reti avversarie generative
Il metodo di addestramento “indiretto
L’approccio “diretto” presentato in precedenza confronta direttamente la distribuzione generata con quella vera quando addestra la rete generativa. L’idea geniale che governa le GAN consiste nel sostituire questo confronto diretto con uno indiretto, che assume la forma di un compito a valle su queste due distribuzioni. L’addestramento della rete generativa viene quindi effettuato rispetto a questo compito, in modo da forzare la distribuzione generata ad avvicinarsi sempre di più alla distribuzione vera.
Il compito a valle delle GAN è un compito di discriminazione tra i campioni veri e quelli generati. O potremmo dire un compito di “non discriminazione”, poiché vogliamo che la discriminazione fallisca il più possibile. Quindi, in un’architettura GAN, abbiamo un discriminatore, che prende campioni di dati veri e generati e che cerca di classificarli il meglio possibile, e un generatore che viene addestrato per ingannare il più possibile il discriminatore.
Vediamo con un semplice esempio perché gli approcci diretti e indiretti di cui abbiamo parlato dovrebbero, in teoria, portare allo stesso generatore ottimale.
Il caso ideale: generatore e discriminatore perfetti
Per capire meglio perché l’addestramento di un generatore per ingannare un discriminatore porterà allo stesso risultato dell’addestramento diretto del generatore per far corrispondere la distribuzione target, prendiamo un semplice esempio monodimensionale. Dimentichiamo, per il momento, come sono rappresentati sia il generatore che il discriminatore e li consideriamo come nozioni astratte (che saranno specificate nella prossima sottosezione). Inoltre, si suppone che entrambi siano “perfetti” (con capacità infinite) nel senso che non sono vincolati da alcun tipo di modello (parametrato).
Supponiamo di avere una distribuzione vera, per esempio una gaussiana monodimensionale, e di volere un generatore che campioni da questa distribuzione di probabilità. Quello che chiamiamo metodo di addestramento “diretto” consisterebbe nel regolare iterativamente il generatore (iterazioni di discesa del gradiente) per correggere la differenza/errore misurata tra la distribuzione vera e quella generata. Infine, supponendo che il processo di ottimizzazione sia perfetto, dovremmo ottenere una distribuzione generata che corrisponde esattamente alla distribuzione vera.
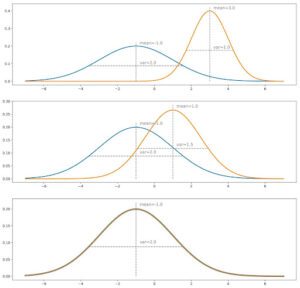
Illustrazione del concetto di metodo di corrispondenza diretta. La distribuzione in blu è quella vera, mentre quella generata è rappresentata in arancione. Iterazione per iterazione, confrontiamo le due distribuzioni e regoliamo i pesi delle reti attraverso passi di discesa del gradiente. In questo caso il confronto avviene sulla media e sulla varianza (simile a un metodo di corrispondenza dei momenti troncati). Si noti che (ovviamente) questo esempio è talmente semplice da non richiedere un approccio iterativo: lo scopo è solo quello di illustrare l’intuizione data in precedenza.
Per l’approccio “indiretto”, dobbiamo considerare anche un discriminatore. Assumiamo per ora che questo discriminatore sia una sorta di oracolo che sa esattamente quali sono le distribuzioni vere e generate e che è in grado, sulla base di questa informazione, di predire una classe (“vera” o “generata”) per ogni punto dato
. Se le due distribuzioni sono molto distanti, il discriminatore sarà in grado di classificare facilmente e con un alto livello di confidenza la maggior parte dei punti che gli presentiamo. Se vogliamo ingannare il discriminatore, dobbiamo avvicinare la distribuzione generata a quella vera. Il discriminatore avrà maggiori difficoltà a prevedere la classe quando le due distribuzioni saranno uguali in tutti i punti: in questo caso, per ogni punto ci sono uguali possibilità che sia “vero” o “generato” e quindi il discriminatore non può fare meglio che essere vero in un caso su due in media.
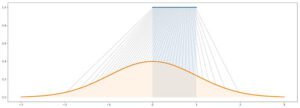
Intuizione per il metodo adversariale. La distribuzione blu è quella vera, quella arancione è quella generata. In grigio, con l’asse delle ordinate corrispondente a destra, abbiamo visualizzato la probabilità che il discriminatore sia vero se sceglie la classe con la densità maggiore in ogni punto (assumendo che i dati “veri” e “generati” siano in proporzioni uguali). Più le due distribuzioni sono vicine, più spesso il discriminatore si sbaglia. Durante l’addestramento, l’obiettivo è quello di “spostare l’area verde” (la distribuzione generata è troppo alta) verso l’area rossa (la distribuzione generata è troppo bassa).
A questo punto, sembra legittimo chiedersi se questo metodo indiretto sia davvero una buona idea. Infatti, sembra essere più complicato (dobbiamo ottimizzare il generatore in base a un compito a valle invece che direttamente in base alle distribuzioni) e richiede un discriminatore che qui consideriamo come un oracolo dato ma che in realtà non è né noto né perfetto. Per quanto riguarda il primo punto, la difficoltà di confrontare direttamente due distribuzioni di probabilità basate su campioni controbilancia l’apparente maggiore complessità del metodo indiretto. Per il secondo punto, è ovvio che il discriminatore non è noto. Tuttavia, può essere appreso!
L’approssimazione: le reti neurali avversarie
Descriviamo ora la forma specifica che assumono il generatore e il discriminatore nell’architettura delle GAN. Il generatore è una rete neurale che modella una funzione di trasformazione. Prende in input una semplice variabile casuale e deve restituire, una volta addestrata, una variabile casuale che segue la distribuzione desiderata. Poiché è molto complicato e sconosciuto, decidiamo di modellare il discriminatore con un’altra rete neurale. Questa rete neurale modella una funzione discriminante. Prende in input un punto (nell’esempio del cane un vettore di N dimensioni) e restituisce in output la probabilità che questo punto sia un punto “vero”.
Si noti che il fatto di imporre ora un modello parametrico per esprimere sia il generatore che il discriminatore (invece delle versioni idealizzate della sottosezione precedente) non ha, in pratica, un impatto enorme sull’argomentazione/intuizione teorica data sopra: semplicemente, lavoriamo in alcuni spazi parametrici invece che in spazi pieni ideali e, quindi, i punti ottimali che dovremmo raggiungere nel caso ideale possono essere visti come “arrotondati” dalla capacità di precisione dei modelli parametrici.
Una volta definite, le due reti possono essere addestrate congiuntamente (contemporaneamente) con obiettivi opposti:
– l’obiettivo del generatore è quello di ingannare il discriminatore, quindi la rete neurale generativa viene addestrata per massimizzare l’errore di classificazione finale (tra dati veri e dati generati)
– l’obiettivo del discriminatore è individuare i dati generati falsi, quindi la rete neurale discriminativa viene addestrata per minimizzare l’errore di classificazione finale.
Quindi, a ogni iterazione del processo di addestramento, i pesi della rete generativa vengono aggiornati in modo da aumentare l’errore di classificazione (errore a gradiente ascendente sui parametri del generatore), mentre i pesi della rete discriminativa vengono aggiornati in modo da diminuire questo errore (errore a gradiente discendente sui parametri del discriminatore).
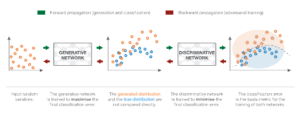
Rappresentazione delle reti avversarie generative. Il generatore prende in input semplici variabili casuali e genera nuovi dati. Il discriminatore prende i dati “veri” e quelli “generati” e cerca di discriminarli, costruendo un classificatore. L’obiettivo del generatore è quello di ingannare il discriminatore (aumentare l’errore di classificazione mescolando il più possibile i dati generati con quelli veri), mentre l’obiettivo del discriminatore è quello di distinguere tra i dati veri e quelli generati.
Questi obiettivi opposti e l’implicita nozione di addestramento avversario delle due reti spiegano il nome di “reti avversarie”: entrambe le reti cercano di battersi a vicenda e, così facendo, diventano sempre migliori. La competizione tra le due reti le fa “progredire” rispetto ai rispettivi obiettivi. Da un punto di vista della teoria dei giochi, possiamo pensare a questa impostazione come a un gioco minimax a due giocatori, in cui lo stato di equilibrio corrisponde alla situazione in cui il generatore produce dati dall’esatta distribuzione mirata e in cui il discriminatore predice “vero” o “generato” con probabilità 1/2 per ogni punto che riceve.
Dettagli matematici sulle GAN
Nota: questa sezione è un po’ più tecnica e non è assolutamente necessaria per la comprensione generale delle GAN. Quindi, i lettori che non vogliono leggere subito un po’ di matematica possono saltare questa sezione per il momento. Per gli altri, vediamo come vengono formalizzate matematicamente le intuizioni date sopra.
Disclaimer: le equazioni riportate di seguito non sono quelle dell’articolo di Ian Goodfellow. Proponiamo qui un’altra formalizzazione matematica per due motivi: primo, per rimanere un po’ più vicini alle intuizioni date sopra e, secondo, perché le equazioni dell’articolo originale sono già così chiare che non sarebbe stato utile riscriverle. Si noti inoltre che non entriamo assolutamente nel merito delle considerazioni pratiche (gradiente di vanificazione o altro) relative alle diverse funzioni di perdita possibili. Invitiamo caldamente il lettore a dare un’occhiata anche alle equazioni dell’articolo originale: la differenza principale è che Ian Goodfellow e coautori hanno lavorato con l’errore di cross-entropia invece che con l’errore assoluto (come facciamo noi). Inoltre, nel seguito assumiamo un generatore e un discriminatore con capacità illimitata.
La modellazione delle reti neurali richiede essenzialmente la definizione di due elementi: un’architettura e una funzione di perdita. Abbiamo già descritto l’architettura delle reti avversarie generative. Essa consiste in due reti:
– una rete generativa G(.) che prende un input casuale z con densità p_z e restituisce un output x_g = G(z) che dovrebbe seguire (dopo l’addestramento) la distribuzione di probabilità desiderata
– una rete discriminativa D(.) che prende un input x che può essere un dato “vero” (x_t, la cui densità è indicata con p_t) o un dato “generato” (x_g, la cui densità p_g è la densità indotta dalla densità p_z che passa attraverso G) e che restituisce la probabilità D(x) che x sia un dato “vero”.
Vediamo ora da vicino la funzione di perdita “teorica” delle GAN. Se inviamo al discriminatore dati “veri” e “generati” nelle stesse proporzioni, l’errore assoluto atteso del discriminatore può essere espresso come
L’obiettivo del generatore è quello di ingannare il discriminatore, che deve essere in grado di distinguere tra dati veri e dati generati. Pertanto, durante l’addestramento del generatore, vogliamo massimizzare questo errore, mentre cerchiamo di ridurlo al minimo per il discriminatore. Questo ci dà
Per un dato generatore G (insieme alla densità di probabilità indotta p_g), il miglior discriminatore possibile è quello che minimizza
Per minimizzare (rispetto a D) questo integrale, possiamo minimizzare la funzione all’interno dell’integrale per ogni valore di x. Essa definisce quindi il miglior discriminatore possibile per un dato generatore
(in realtà, uno dei migliori perché i valori di x tali che p_t(x)=p_g(x) potrebbero essere gestiti in un altro modo, ma non ha importanza per quanto segue). Cerchiamo quindi G che massimizzi
Ancora una volta, per massimizzare (rispetto a G) questo integrale, possiamo massimizzare la funzione all’interno dell’integrale per ogni valore di x. Poiché la densità p_t è indipendente dal generatore G, non possiamo fare di meglio che impostare G in modo tale che
Naturalmente, poiché p_g è una densità di probabilità che deve integrare a 1, si ha necessariamente per il migliore G
Abbiamo quindi dimostrato che, in un caso ideale con generatore e discriminatore a capacità illimitata, il punto ottimale dell’impostazione avversaria è tale che il generatore produce la stessa densità della densità vera e il discriminatore non può fare di meglio che essere vero in un caso su due, proprio come ci diceva l’intuizione. Infine, notiamo anche che G massimizza
In questa forma, vediamo meglio che G vuole massimizzare la probabilità attesa che il discriminatore sia sbagliato.
Conclusioni
I principali insegnamenti di questo articolo sono:
– i computer possono fondamentalmente generare semplici variabili pseudocasuali (ad esempio possono generare variabili che seguono molto da vicino una distribuzione uniforme)
– esistono diversi modi per generare variabili casuali più complesse, tra cui la nozione di “metodo di trasformazione” che consiste nell’esprimere una variabile casuale come funzione di una o più variabili casuali più semplici
– nell’apprendimento automatico, i modelli generativi cercano di generare dati da una data distribuzione di probabilità (complessa)
– i modelli generativi di deep learning sono modellati come reti neurali (funzioni molto complesse) che prendono in input una variabile casuale semplice e restituiscono una variabile casuale che segue la distribuzione desiderata (come il “metodo della trasformazione”)
– queste reti generative possono essere addestrate “direttamente” (confrontando la distribuzione dei dati generati con la distribuzione vera): questa è l’idea delle reti generative di corrispondenza (Generative Matching Networks)
– queste reti generative possono essere addestrate anche “indirettamente” (cercando di ingannare un’altra rete che viene addestrata nello stesso momento per distinguere i dati “generati” da quelli “veri”): è l’idea delle Reti Generative Avversarie.
Anche se il “clamore” che circonda le GAN è forse un po’ esagerato, possiamo dire che l’idea dell’addestramento adversariale proposta da Ian Goodfellow e dai suoi coautori è davvero ottima. Questo modo di stravolgere la funzione di perdita per passare da un confronto diretto a uno indiretto è davvero qualcosa che può essere di grande ispirazione per ulteriori lavori nell’area del deep learning. Per concludere, diciamo che non sappiamo se l’idea delle GAN sia davvero “l’idea più interessante degli ultimi 10 anni nel Machine Learning”… ma è abbastanza ovvio che è, almeno, una delle più interessanti!
Grazie per aver letto!
Articolo originale di Joseph Rocca
Comprendere le reti avversarie generative (GAN)
Understanding Generative Adversarial Networks (GANs) | by Joseph Rocca | Towards Data Science
Share: