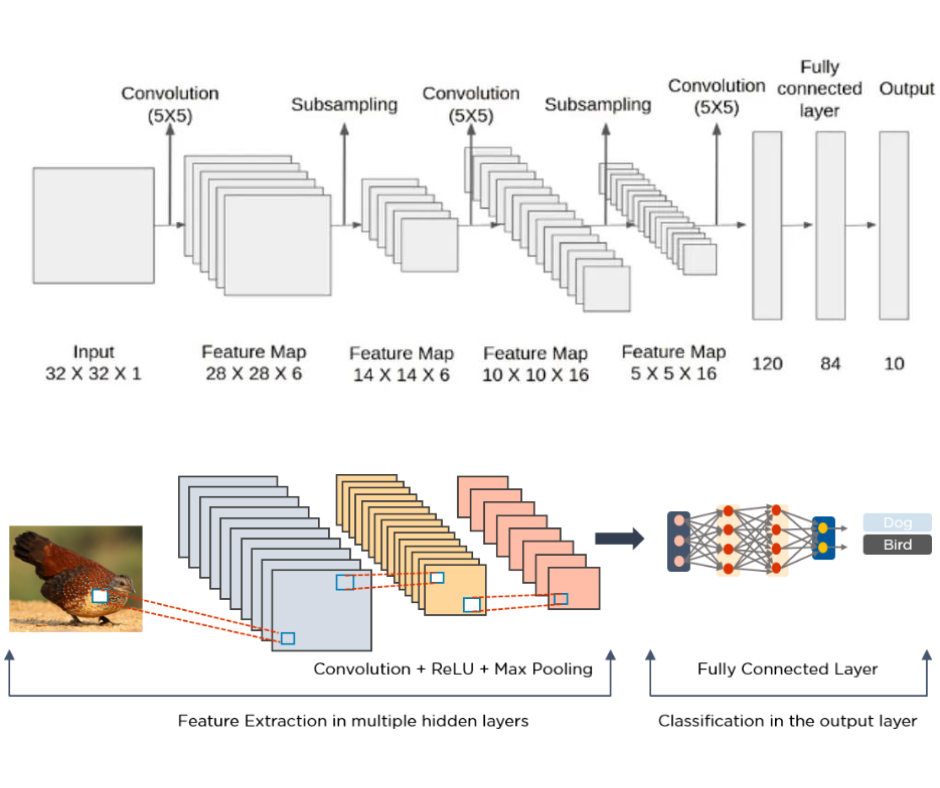
Comprendere le reti convoluzionali (LeNet)
Articolo in lingua originale di Jeremy
Definizione
Le reti neurali convoluzionali (CNNs) sono state costruite per elaborare dati di tipo immagine. L’idea chiave alla base delle CNN è l’addestramento di un modello che impari i kernel che vengono convoluti su un’immagine, identificando pattern che aiutano il modello ad eseguire un certo task. Nell’esempio qua sopra vediamo una CNN utilizzata per classificare l’immagine secondo l’animale che rappresenta.
Motivazione
Vediamo perchè un modello MLP (MultiLayer Perceptron) standard affronterebbe dei problemi con questo tipo di task.

Per passare l’immagine come input, dobbiamo prima appiattirla in una riga, come mostrato sopra. Supponiamo che il quadrato 2 x 2 in basso a destra dell’immagine precedente assomigli a una testa. Nell’immagine appiattita, il modello non dispone più di questa informazione spaziale, poiché ogni pixel viene passato singolarmente.
Sebbene il teorema dell’approssimazione universale dimostri che è possibile per una MLP apprendere queste informazioni spaziali e raggiungere le stesse prestazioni di una CNN, nella pratica le risorse di calcolo e il tempo non sono infinite. Progettando la rete neurale in modo da preservare l’informazione spaziale, le CNN ottengono risultati migliori delle MLP per le immagini, a parità di risorse.
Convoluzione
La convoluzione è un’operazione matematica applicata a due funzioni per produrne una terza che esprime come la prima funzione viene modificata dalla seconda. Viene indicata come:
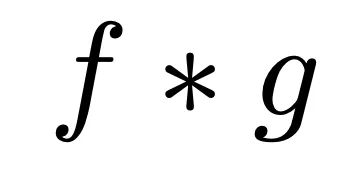
Nel caso di una rete neurale, f è la funzione che mappa i valori dei pixel di un’immagine e g è la funzione che viene applicata ad f e mappa i valori dei pixel dell’immagine in nuovi valori.
Mentre g potrebbe essere realizzata in diversi modi, nel caso di una CNNs g è rappresentata con un kernel. Vediamo un esempio per rendere il tutto più chiaro.
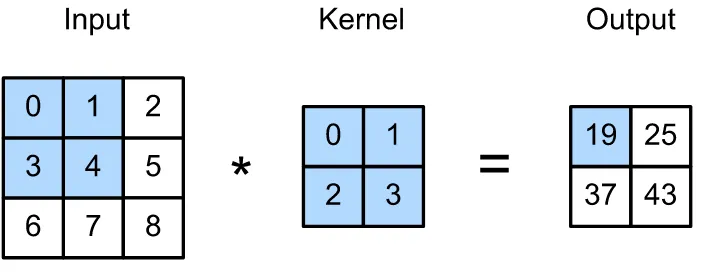
Nell’immagine soprastante abbiamo un’immagine 3×3 e un kernel 2×2. Quando convolgiamo il kernel sull’immagine, attraversiamo ciascuna posizione dell’input e moltiplichiamo ciascuna cella dell’input con quella corrispondente nel kernel.
Il nostro output nell’angolo in alto a sinistra viene calcolato come 0*0 + 1*1 + 3*2 + 4*3 = 19. Successivamente trasliamo il kernel a destra di una casella e applichiamo la stessa operazione: 1*0 + 2*1 + 4*2 + 5*3 = 25. Dal momento che abbiamo raggiunto la fine della cella nel senso della larghezza ci spostiamo in basso di uno e a sinistra per ricominciare dalla cella più a sinistra. Ora calcoliamo: 3*0 + 4*1 + 6*2 + 7*3 = 37. Infine ci spostiamo a destra di uno e calcoliamo: 4*0 + 5*1 + 7*2 + 8*3 = 43. Ora che abbiamo raggiunto l’angolo in basso a destra abbiamo finito.
L’entità di quanto spostiamo il kernel viene definita come “stride”. L’operazione che applichiamo a ogni passo è nota come sum pooling, poiché moltiplichiamo l’immagine per il kernel in ogni cella e sommiamo il risultato. Un approccio alternativo è il max pooling dove, invece di sommare i risultati cella per cella, si prende il valore della cella che ha il valore più alto.
Concetto della convoluzione
Per capire meglio perchè le convoluzioni sono una buona idea, dobbiamo capire i diversi effetti di kernel diversi convoluti su un’immagine.
def convolve(image, kernel, padding=0, strides=1):
kernel_height = kernel.shape[0]
kernel_width = kernel.shape[1]
img_height = image.shape[0]
img_width = image.shape[1]
output_height = int(((img_height - kernel_height + 2 * padding) / strides) + 1)
output_width = int(((img_width - kernel_width + 2 * padding) / strides) + 1)
output = np.zeros((output_height, output_width))
if padding != 0:
imagePadded = np.zeros((img_height + padding*2, img_width + padding*2))
imagePadded[int(padding):int(-1 * padding), int(padding):int(-1 * padding)] = image
else:
imagePadded = image
for i in range(0, img_height-kernel_height+1, strides):
for j in range(0, img_width-kernel_width+1, strides):
vals = []
for k in range(kernel_height):
for l in range(kernel_width):
vals.append(kernel[k][l] * imagePadded[i+k, j+l])
output[i][j] = np.array(vals).sum()
return output
img = train_X[1:2]
plt.figure(figsize=(20,15))
plt.subplot(8,8,1)
plt.imshow(img[0,:,:,0], cmap='gray')
plt.title("Original")
plt.subplot(8,8,2)
kernel = np.array([[1, 1, 1], [1, 1, 1], [1, 1, 1]])
blur_img = convolve(np.reshape(img, (32, 32)), kernel)
plt.imshow(blur_img, cmap='gray')
plt.title("Blurred")
plt.subplot(8,8,3)
kernel = np.array([[1, 0, -1], [1, 0, -1], [1, 0, -1]])
edge_img = convolve(np.reshape(img, (32, 32)), kernel)
plt.imshow(edge_img, cmap='gray')
plt.title("Edges")
plt.show()

Dall’immagine possiamo vedere gli effetti prodotti da kernel diversi. Un kernel 3×3 costituito da soli 1 produce un effetto di sfocatura, mentre un kernel 3×3 [[1,0,-1],[1,0,-1],[1,0,-1]] accentua i contorni.
Ora, invece che impostare manualmente i valori dei kernel, cosa succederebbe se una rete neurale imparasse a costruire i kernel come parte della back-propagation? Il modello impara quali filtri applicare per accentuare gli aspetti chiavi dell’immagine in input in modo da agevolare la previsione.
Per lo stesso input, il modello impara kernel diversi in ciascun layer intermedio. Il numero di kernel imparati viene impostato dal parametro filters.
Concetto di pooling
Dopo il layer di convoluzione, le CNN utilizzano il pooling per ridurre la dimensionalità dell’input passato ai layer successivi. L’intento del pooling è quello di ridurre il numero di parametri, riassumendo al contempo ciò che accade in quella finestra dell’immagine. Si tratta di una forma di regolarizzazione che aiuta il modello a generalizzare.
Vediamo di seguito che il pooling 2×2 conserva per lo più l’immagine originale, pur dimezzando l’altezza e la larghezza dell’immagine. Infine, gli ultimi strati di una CNN sono costituiti da strati densi ai quali viene passato l’output dell’immagine convoluta. Riducendo l’immagine di un fattore 4 (dimezzando la larghezza e l’altezza), riduciamo di un fattore 4 il numero di parametri in questo o questi strati densi finali.
def pool(image, pool_size, pool_type):
height, width = image.shape[0], image.shape[1]
output = np.zeros((height, width))
for i in range(height-pool_size[0]+1):
for j in range(width-pool_size[1]+1):
vals = []
for k in range(pool_size[0]):
for l in range(pool_size[1]):
vals.append(image[i+k][j+l])
if pool_type == MAX_POOL:
output[i][j] = max(vals)
elif pool_type == SUM_POOL:
output[i][j] = sum(vals)
elif pool_type == AVG_POOL:
output[i][j] = sum(vals)/len(vals)
else:
output[i][j] = image[i][j]
return output
img = train_X[1:2]
MAX_POOL = 1
SUM_POOL = 2
AVG_POOL = 3
plt.figure(figsize=(20,15))
plt.subplot(8,8,1)
plt.imshow(img[0,:,:,0], cmap='gray')
plt.title("Original")
plt.subplot(8,8,2)
max_img = pool(np.reshape(img, (32, 32)), (2, 2), MAX_POOL)
plt.imshow(max_img, cmap='gray')
plt.title("Max pool")
plt.subplot(8,8,3)
sum_img = pool(np.reshape(img, (32, 32)), (2, 2), SUM_POOL)
plt.imshow(sum_img, cmap='gray')
plt.title("Sum pool")
plt.subplot(8,8,4)
avg_img = pool(np.reshape(img, (32, 32)), (2, 2), AVG_POOL)
plt.imshow(avg_img, cmap='gray')
plt.title("Avg pool")
plt.show()

Costruire una CNN
La rete LeNet realizzata nel 1998 è una delle prime reti neurali convoluzionali mai costruite. Implementiamo questo modello utilizzando Keras per capire cosa succede!
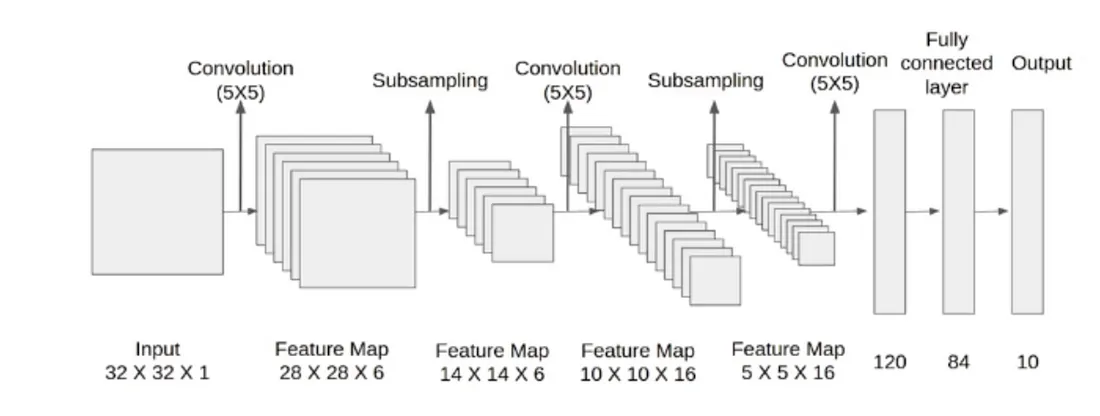
Addestreremo questo modello utilizzando il famoso dataset MNIST su 60mila esempi.
model = Sequential([ Reshape((32, 32, 1)), Convolution2D(filters=6, kernel_size=(5,5), activation='tanh'), AveragePooling2D(pool_size=(2,2)), Convolution2D(filters=16, kernel_size=(5,5), activation='tanh'), AveragePooling2D(pool_size=(2,2)), Convolution2D(filters=120, kernel_size=(5,5), activation='tanh'), Flatten(), Dense(84, activation='tanh'), Dense(10, activation='softmax') ]) model.compile(optimizer="Adam", loss="categorical_crossentropy", metrics=["accuracy"]) results = model.fit(x=train_X, y=train_y, batch_size=64, validation_split=0.1, epochs=10) model.summary()
Valutando questo modello su un test set tenuto da parte, raggiunge il 98% di accuracy.
Guardiamo ora il numero di parametri e le dimensioni finali di ciascun layer per capire come appare questa rete:
- Da conv2d ci aspetteremmo di avere 5*5*6=150 parametri come risultato dell’altezza/larghezza del kernel e della specifica che vogliamo imparare 6 filtri/kernel. I 6 parametri aggiuntivi derivano dal termine bias associato a ciascun kernel appreso. La forma in uscita riduce la larghezza/altezza di 4 come risultato dell’applicazione di ciascun kernel sull’immagine. Invece di un’immagine, ora abbiamo 6 immagini che sono il risultato dell’applicazione di ciascun kernel appreso separatamente su un’immagine.
- average_pooling2d dimezza quindi le dimensioni di larghezza/altezza dell’output di conv2d. Non ci sono parametri che il modello apprende in questo caso.
- Successivamente conv2d_1 prende l’output del livello precedente e apprende 16 filtri/kernel. Intuitivamente si potrebbe pensare che apprendiamo 16 kernel per ciascuna delle 6 uscite dei filtri, ottenendo 96 uscite. Invece vediamo che l’uscita di questo livello è 16. Ciò che accade è che conv2d applica un kernel 3D di dimensioni (5,5,6) convoluto sulle uscite del livello precedente. Ogni uscita dello strato precedente viene raggruppata per formare un cubo di dimensioni (14,14,6) e questo viene trattato come “immagine” a cui viene applicata la convoluzione. Impariamo quindi 16 di questi kernel 3D, ottenendo 16*5*5*6+16=2416 parametri. Si noti che il risultato della convoluzione di un kernel 3D su un'”immagine” 3D sarà ancora 2D quando la dimensione della terza dimensione è uguale tra kernel e immagine (come in questo caso).
- Anche in questo caso utilizziamo average_pooling2d_1 per dimezzare la dimensione di uscita.
- Quindi applichiamo l’ultima convoluzione in conv2d_2. Poiché l’output del livello precedente aveva altezza/larghezza = 5 e i kernel appresi in questo livello hanno altezza/larghezza = 5, l’output di questo livello è un singolo valore. Ci sono 120 valori perché in questo livello vengono appresi 120 kernel. Poiché stiamo applicando un kernel 3d di dimensioni (5,5,16) e vogliamo impararne 120, il numero di parametri necessari è 120*5*5*16+120=48120.
- Infine, appiattiamo (flatten) il nostro output e applichiamo alcuni strati densi completamente connessi per ottenere l’output a 10 dimensioni corrispondente a ogni possibile classe di output. Il numero di parametri per dense si ottiene con 120*84+84=10164 e per dense_1 con 84*10+10=850.
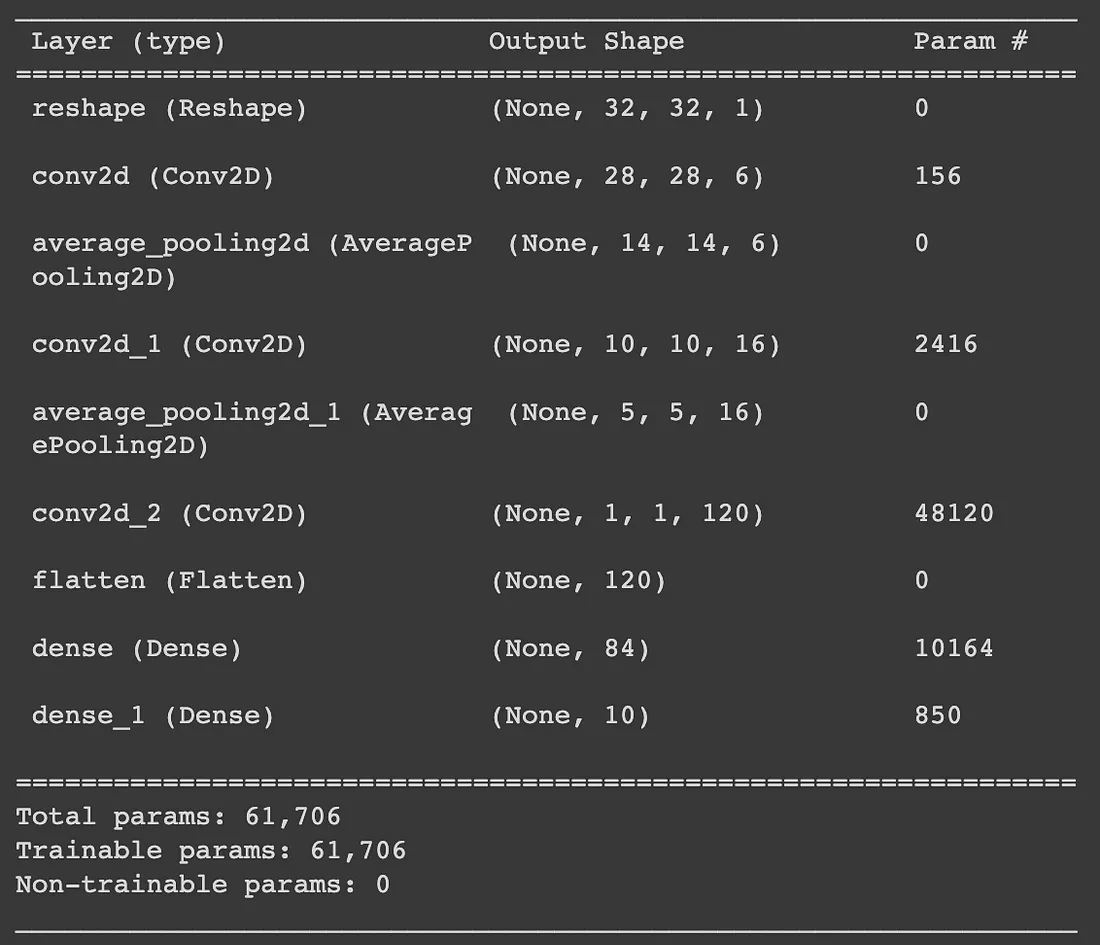
Per comprendere cosa il modello consideri come caratteristiche chiave che lo aiutino nella previsione, possiamo visualizzare i kernel/filtri che il modello ha imparato.
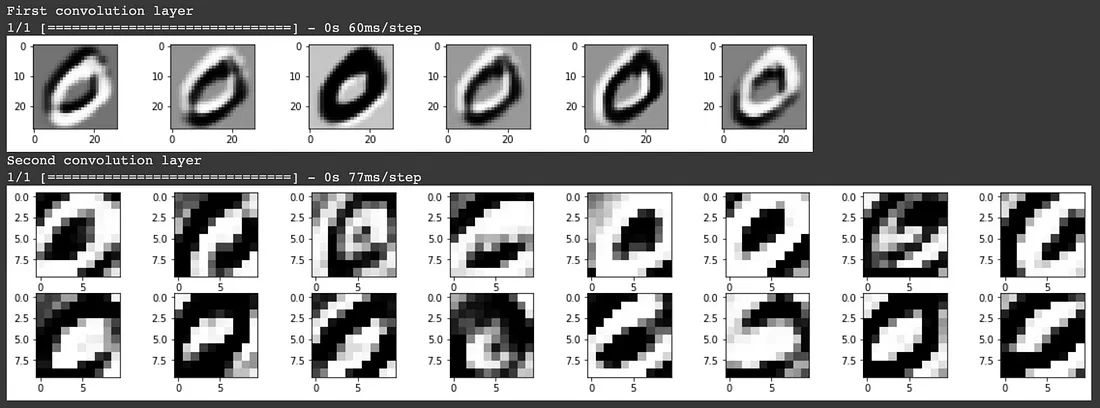
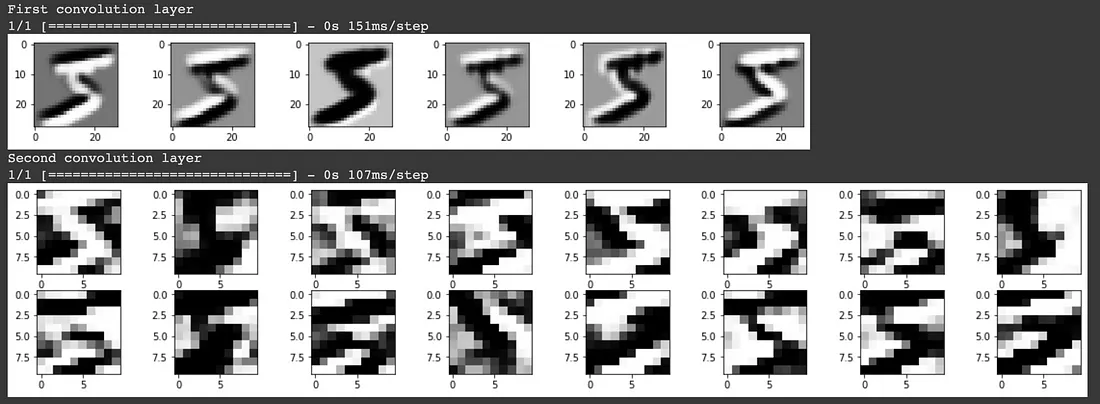
Nel primo layer di convoluzione, vediamo che il modello ha conservato in gran parte l’immagine di ingresso e sembra aver appreso dei filtri che identificano i bordi. Nel secondo layer di convoluzione è meno chiaro cosa rappresentino questi filtri. Questo è il risultato dell’applicazione di un kernel 3D su ciascuna delle uscite del livello di convoluzione precedente. Sebbene noi esseri umani non possiamo capire facilmente cosa rappresenti, il modello è in grado di utilizzare questo input per ottenere un elevato punteggio di accuratezza nella classificazione delle immagini.
L’idea della convoluzione del kernel 3D non è evidente dall’output del primo livello di convoluzione, poiché l’immagine in ingresso era una sola. Nel caso in cui l’input sia un’immagine a colori RGB composta da 3 canali, si applicherebbe un kernel 3D nel primo livello di convoluzione, mentre i livelli di convoluzione successivi applicherebbero un kernel 4D.
Potete trovare i notebook di tutto il codice qui.
Share: