Cos’è una rete generativa avversaria? (Generative Adversarial Network, GAN)
Cosa è un modello generativo?
Articolo originale in lingua inglese di Hunter Heidenreich
Prima ancora di iniziare a parlare di reti generative avversarie (GAN), vale la pena chiedersi cosa sia un modello generativo. Perché mai dovremmo volere una cosa del genere? Qual è l’obiettivo? Queste domande possono prepararci ad affrontare meglio le GAN.
Quindi perché vogliamo un modello generativo? Beh, la risposta possiamo trovarla nel nome! Vogliamo generare qualcosa. Ma che cosa? Tipicamente, vogliamo generare dati (Lo so, non molto specifico). Ma soprattutto, è probabile che ci interessi generare dati mai visti prima, ma che comunque rientrino in una certa distribuzione di dati (ovvero una sorta di set di dati predefiniti che abbiamo già messo da parte).
E qual è l’obiettivo di un tale modello generativo? Diventare così bravo a tirar fuori nuovi contenuti generati che noi (o qualsiasi altro sistema che osserva i campioni) non siamo più in grado di distinguere quali campioni siano originali e quali, invece, generati. Una volta che abbiamo un sistema in grado di arrivare a tanto, siamo liberi di iniziare a generare nuovi campioni mai visti prima d’ora, ma comunque credibili rispetto ai dati reali.
Per andare più a fondo della questione, vogliamo che il modello generativo sia in grado di stimare accuratamente la distribuzione di probabilità dei dati reali. Diremo che, considerando un parametro W, vorremmo trovare quel parametro che massimizzi la verosimiglianza dei campioni reali. Addestrando il modello generativo, questo parametro ideale W lo si trova minimizzando la distanza tra la stima della distribuzione dei dati e la distribuzione effettiva.
Una buona misura della distanza tra le distribuzioni è la divergenza di Kullback-Leibler, è dimostrato che massimizzare la verosimiglianza logaritmica è equivalente a minimizzare questa distanza. Considerando il nostro modello generativo parametrizzato e minimizzandone la distanza con la distribuzione dei dati reali significa creare un buon modello generativo.
Questo ci porta anche a definire due diversi modelli generativi.
Modelli generativi a distribuzione esplicita
Un modello generativo a distribuzione esplicita nasce da una distribuzione del modello generativo definita esplicitamente. Successivamente la stima parametrizzata esplicitamente definita viene poi affinata attraverso l’addestramento su campioni di dati.
Un esempio di modello generativo a distribuzione esplicita è un Variational Auto-Encoder (VAE).
I VAE necessitano di una distribuzione definita esplicitamente a priori insieme alla distribuzione di verosimiglianza. Utilizzano queste due componenti per giungere ad un’ approssimazione variazionale con cui valutare come stanno performando. A causa di queste necessità e di questa componente, i VAEs devono essere distribuiti esplicitamente.
Modelli generativi a distribuzione implicita
Proprio come avrete già intuito, i modelli generativi a distribuzione implicita non richiedono una definizione esplicita della loro distribuzione. Al contrario, questi modelli si addestrano da soli campionando indirettamente i dati dalla propria distribuzione parametrizzata. E come potete aver già capito, questo è ciò che fa una GAN.
Ma come lo fa esattamente? Andiamo più a fondo dell’argomento e iniziamo a delineare il quadro della situazione.
Comprensione ad alto livello delle GAN
Le reti avversarie generative sono costituite da tre componenti. Abbiamo accennato all’aspetto generativo mentre quello di rete si spiega pressoché da sé. Ma cosa dire della componente avversaria?
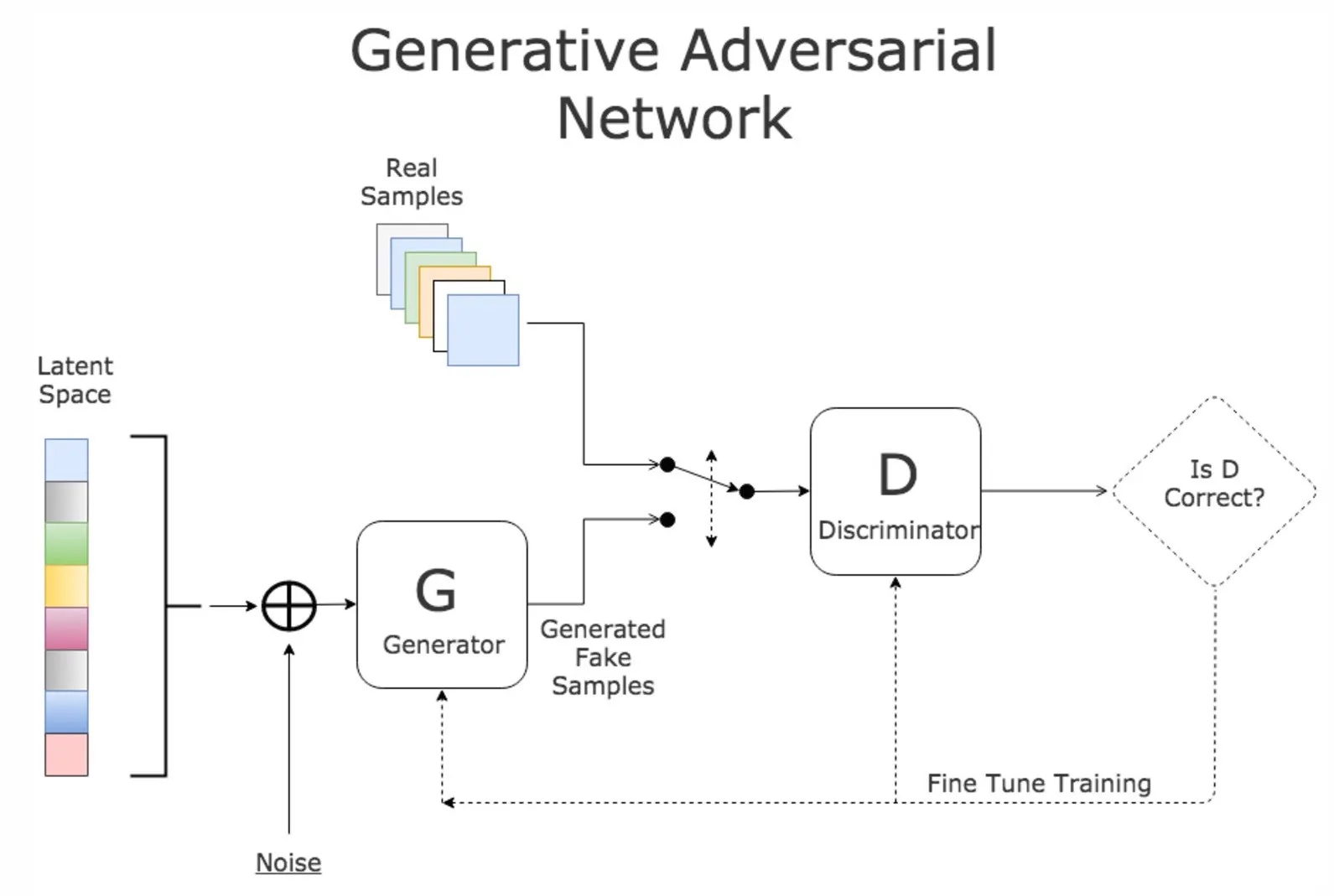
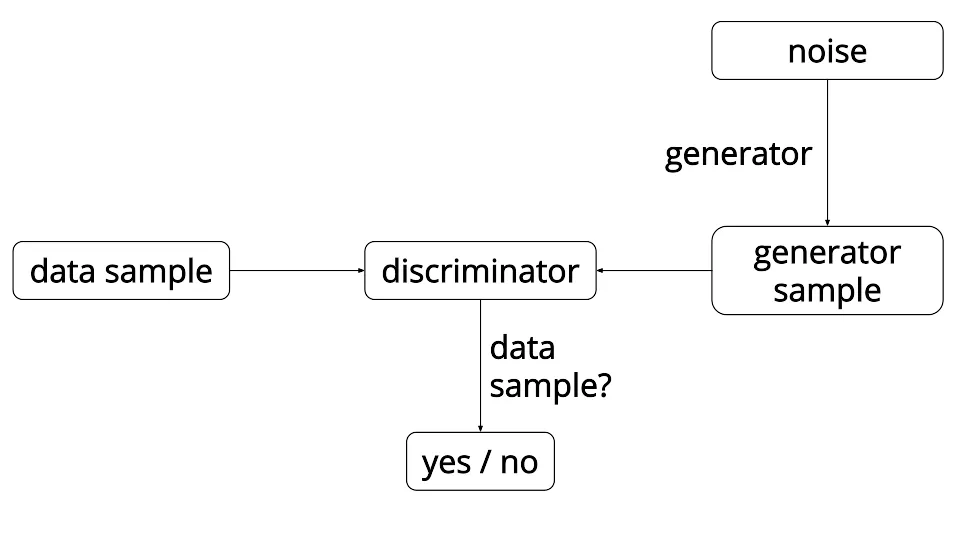
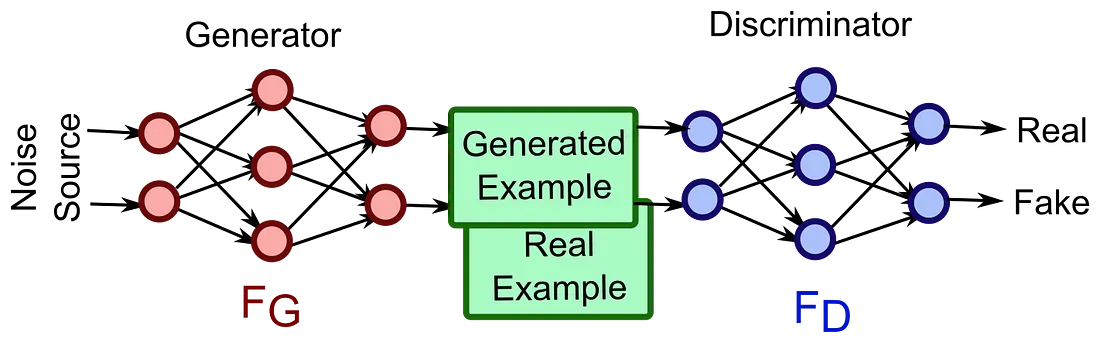
Beh, le GAN hanno due componenti che costituiscono la loro rete: un generatore G ed un discriminatore D. Queste due componenti costituiscono la rete e lavorano come avversarie, spingendo una le prestazioni dell’altra.
Generatore e Discriminatore
Generatore
Il generatore è responsabile della produzione di falsi esempi di dati. Prende in input una variabile latente (che chiameremo z) e produce dati che hanno la stessa forma di quelli del set di dati originale.
Le variabili latenti sono variabili nascoste. Quando si parla di GAN, abbiamo questo concetto di “spazio latente” da cui possiamo campionare.
Possiamo scorrere continuamente attraverso questo spazio latente che, quando si dispone di una GAN ben addestrata, avrà effetti sostanziali (e spesso in qualche modo comprensibili) sull’output.
Se la nostra variabile latente è z e la nostra variabile target è x, possiamo pensare al generatore della rete come una componente che apprende una funzione che mappa da z (lo spazio latente) a x (la distribuzione reale dei dati, si spera).
Discriminatore
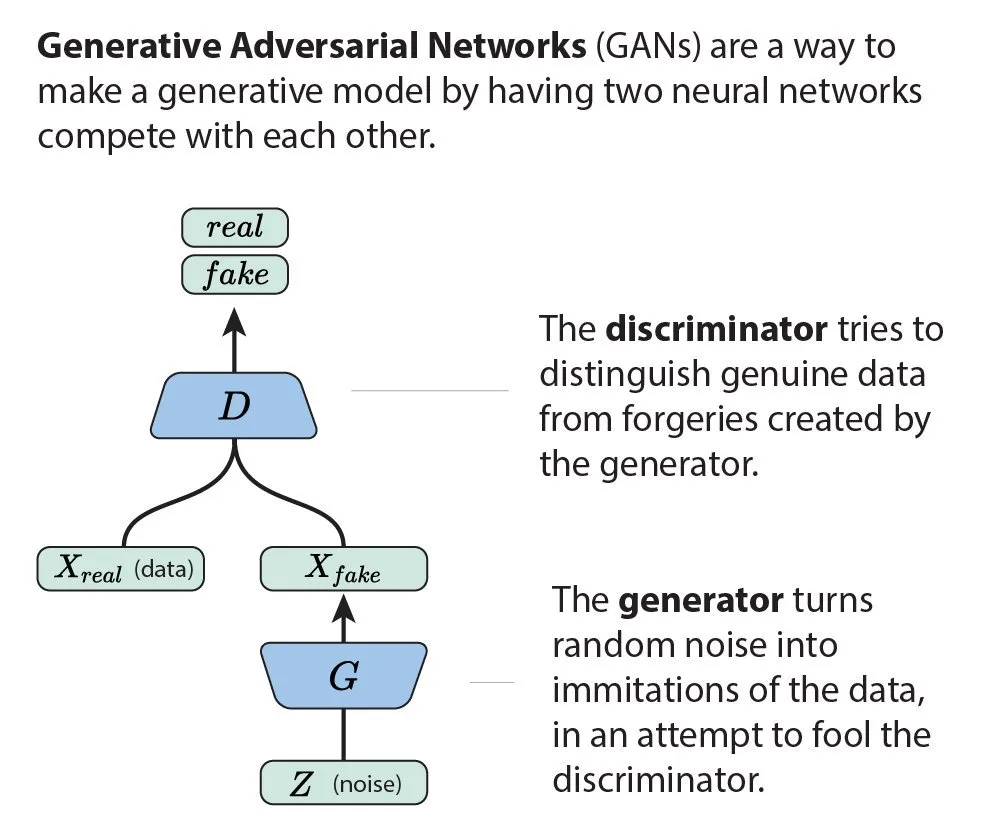
Il ruolo del discriminatore è quello di discriminare. Riceve in input un elenco di campioni e se ne esce con una previsione: se il campione ricevuto è reale o meno. La probabilità in output sarà maggiore più il discriminatore pensa che l’esempio sia reale.
Possiamo pensare al nostro discriminatore coma una sorta di “rilevatore di stron*ate”.
Competizione avversaria
Queste due componenti si incontrano e si sfidano. Il generatore e il discriminatore si oppongono l’uno contro l’altro, provando a massimizzare i propri obiettivi che sono opposti: il generatore spinge per creare campioni che sembrano sempre più simili a quelli reali, mentre il discriminatore vuole riuscire a predire sempre correttamente la provenienza di un campione (reale o generato).
Il fatto che questi obiettivi siano direttamente opposti l’uno all’altro è da dove la GAN ottiene la componente avversaria del suo nome.
A chi non piace una buona metafora per imparare un concetto?
Esempi
Falsificazione dei pezzi d’arte
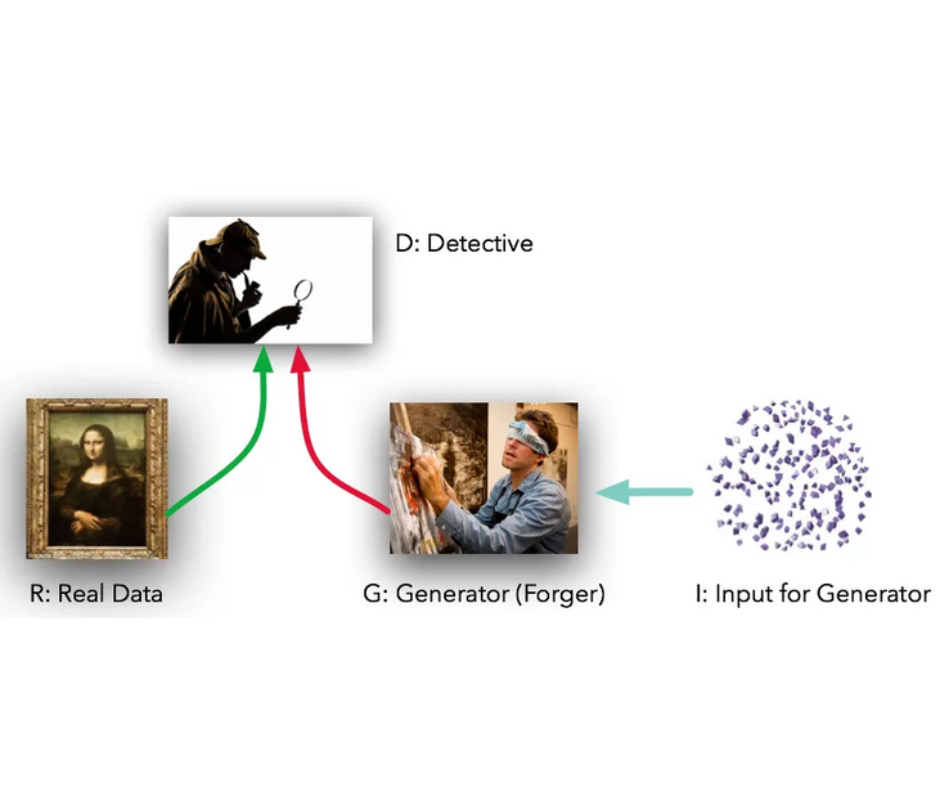
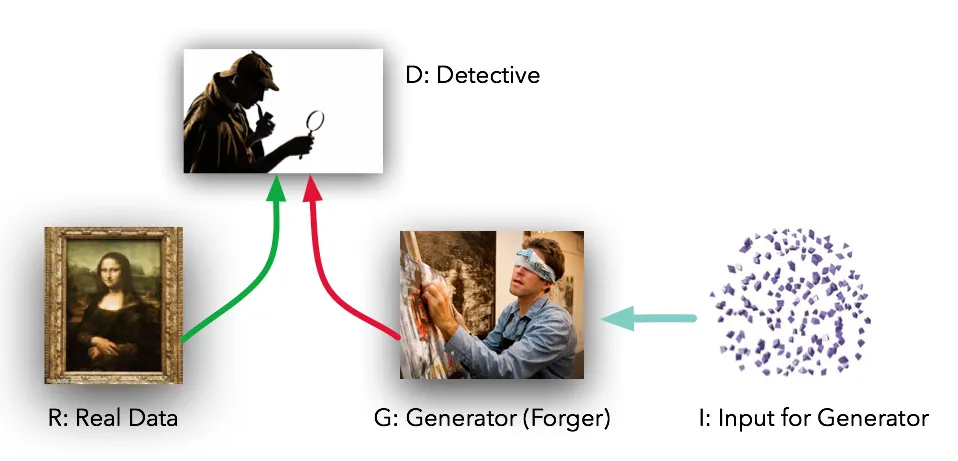
La mia metafora preferita di quanto imparavo per la prima volta delle GANs è quella del falsario contro il critico. In questa metafora il nostro generatore è un criminale che sta provando a falsificare un pezzo d’arte, mentre il discriminatore è un critico d’arte che dovrebbe essere in grado di identificare correttamente se un pezzo è falso o autentico.
I due fanno un po’ tira e molla, in opposizione diretta l’uno all’altro, provando a superarsi a vicenda in quanto il loro lavoro dipende da quello.
Soldi finti
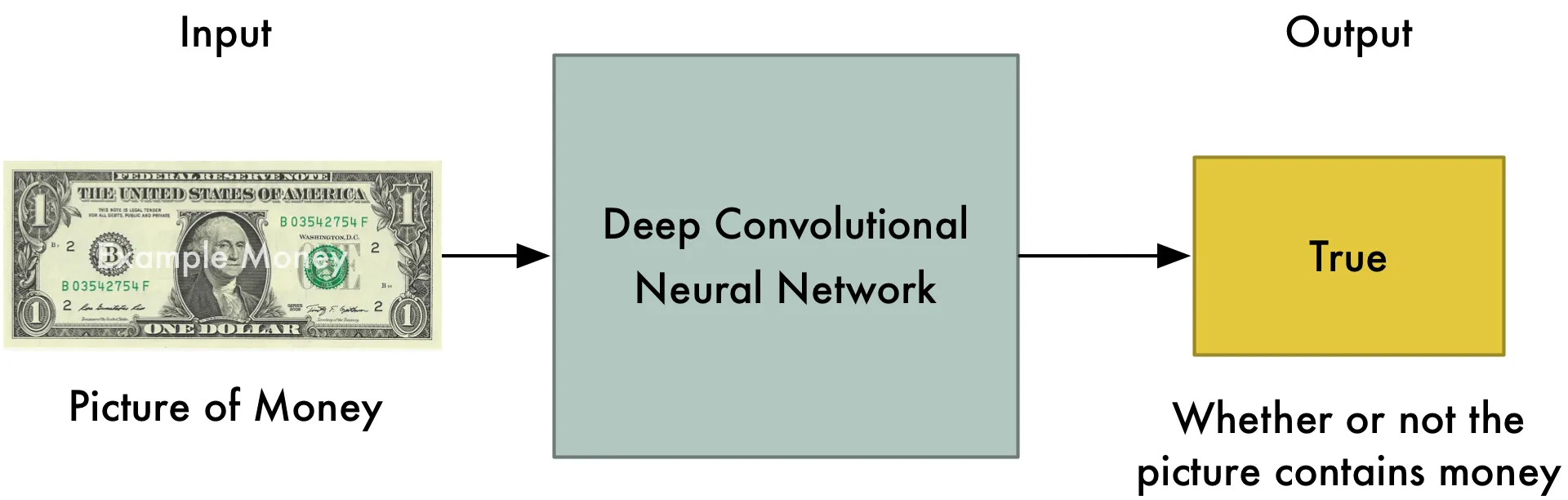
E se invece che un compito di falsificazione di opere d’arte avessimo un criminale che cerca di fabbricare denaro falso e un tirocinante in banca che vuole assicurarsi di non accettare denaro falso?
Forse all’inizio il criminale non sarebbe molto in grado di assolvere bene il suo compito. Quindi giunge in banca e prova a rifilare al tirocinante una banconota con il simbolo del dollaro disegnato a pennarello. (Palesemente un dollaro falso). Però anche il tirocinante potrebbe essere così poco capace nel suo lavoro da far fatica a capire se effettivamente ha tra le mani un falso. Entrambi imparano molto da questa prima interazione. Arriva il giorno seguente in cui il criminale giunge in banca e i suoi soldi finti saranno leggermente migliorati per cui sarà più difficile capire se sono falsi o meno.
Giorno dopo giorno in cui si ripete la stessa cosa, i due diventano davvero bravi a fare il proprio lavoro. Tuttavia, ad un certo punto, potrebbe arrivare un giorno in cui raggiungono una sorta di equilibrio per cui i dollari del criminale sono così realistici che nemmeno un esperto in banca riuscirebbe a dire se sono falsi o meno.
Quello è il giorno in cui il tirocinante viene licenziato, ed è anche il giorno in cui possiamo utilizzare il nostro criminale per diventare veramente ricchi!
Pappagallo
I due esempi precedenti erano incentrati sulla visualizzazione, che ne dite di un esempio un po’ diverso?
Supponiamo che il nostro generatore sia il nostro pappagallo domestico e che il nostro discriminatore sia nostro fratello minore. Ogni giorno, ci sediamo dietro una tenda e il nostro pappagallo si trova, invece, dietro un’altra. Il pappagallo cercherà di imitare la nostra voce per ingannare il fratello minore. Se ci riesce, gli diamo un premio. Se, invece, nostro fratello indovina correttamente dietro quale tenda ci troviamo diamo a lui un premio (si spera uno diverso da quello che diamo al pappagallo).
Forse all’inizio il pappagallo non sarà per niente bravo a mimare la nostra voce. Tuttavia, giorno dopo giorno, con la pratica il pappagallo potrebbe essere capace di sviluppare le abilità per mimare esattamente la nostra voce. A quel punto, avremo addestrato il pappagallo a parlare esattamente come noi e possiamo diventare famosi su internet.
Abbiamo fatto centro!
La matematica dietro al mostro
Prima di concludere questa introduzione alle GANs, vale la pena di approfondire un po’ più nel dettaglio la matematica che sta dietro a una GAN.
Le GAN hanno l’obiettivo di trovare l’equilibrio tra le due metà della loro rete risolvendo la seguente equazione di minimax:
La chiamiamo equazione di minmax perché stiamo cercando di ottimizzare congiuntamente due reti parametrizzate, G e D, per trovare un equilibrio tra le due. Vogliamo massimizzare la confusione di D mentre riduciamo al minimo gli errori di G. Una volta risolta, la nostra distribuzione di dati parametrizzata, implicita e generativa dovrebbe corrispondere abbastanza bene alla distribuzione dei dati originali
Per scomporre ulteriormente le parti della nostra equazione, analizziamola e riflettiamoci su ancora un po’. D vuole massimizzarla: quando riceve in input un campione reale vuole massimizzare l’output, mentre lo vuole minimizzare se in input riceve un campione falso. Questo è essenzialmente il punto di partenza della metà destra dell’equazione. Dall’altro lato, G cerca di ingannare D massimizzando il suo output quando riceve un campione falso. Ecco perché D cerca di massimizzare mentre G di minimizzare.
Ed è proprio dalla minimizzazione/massimizzazione che arriviamo al termine minmax.
Ora, supponiamo che G e D sono ben parametrizzate, ovvero hanno sufficiente capacità di apprendimento, questa equazione di minmax ci aiuta a raggiungere l’equilibrio di Nash tra le due. Questa è la situazione ideale.
Come raggiungere questo risultato?
Semplice: iterando.
Sto scherzando. Non è così semplice, però possiamo descriverlo in modo abbastanza semplice.
Per iniziare, addestriamo innanzitutto D ad essere un buon classificatore tenendo fisso G. A questo punto, fissiamo D e addestriamo G ad ingannare al meglio D. Iterando, possiamo ottimizzare l’equazione di minmax fino al punto in cui D non è più in grado di discriminare tra campioni reali e falsi perché la distribuzione dei dati generati è più o meno indistinguibile da quella della distribuzione dei dati reali.
A questo punto, D ha il 50% di probabilità di indovinare se il campione che riceve è vero o falso.
Tirando le somme
Ecco qua la vostra introduzione alle GANs. Ma ragazzi, c’è ancora molto da fare! Abbiamo appena iniziato a grattare la superficie e abbiamo affrontato tutto ad un livello alto. Tuttavia, ci sono molte altre complessità da affrontare. Non tutto è così semplice come lo abbiamo descritto ora e addestrare una GAN in un ambiente reale può essere veramente difficile. Per questo motivo, approfondiremo in post successivi le componenti delle GANs, i problemi, le scoperte, le varianti e altro ancora. Per ora godetevi il fatto che siete sulla buona strada per capire il magico mondo dei modelli generativi e delle GAN!
Se questo articolo vi è piaciuto o vi è stato utile in qualche modo, vi sarei grato se mi passaste un dollaro o due per contribuire a finanziare la mia formazione e ricerca sull’apprendimento automatico! Ogni dollaro mi aiuta ad avvicinarmi un po’ di più e ve ne sarò sempre grato. E rimanete sintonizzati per altri blog GAN nel prossimo futuro!
P.S. Ringrazio gli autori di How Generative Adversarial Networks and Its Variants Work: An Overview of GAN che hanno contribuito a ispirarmi e a farmi capire meglio come funzionano le GAN. Senza il loro articolo, questa serie non sarebbe stata completamente possibile.Pubblicato originariamente su hunterheidenreich.com.
Share: