Implementare una rete neurale ibrida classico-quantistica con Qiskit
by Parmeet Singh Chani, Hojun Lee, Emilio Peláez, Anuranan Das and Daniel Sierra-Sosa
In questo tutorial ci concentriamo sull’implementazione della rete neurale ibrida quantistico-classica proposta da Rongxin Xia e Sabre Kais utilizzando Qiskit, un software che viene utilizzato anche nelle esercitazioni del nostro corso di Quantum Computing. Questa rete neurale è composta da circuiti quantistici parametrizzati (PQC), ovvero con porte che dipendono da alcuni parametri di ingresso. In primo luogo, definiremo uno schema di codifica dei dati per mappare i dati classici in stati quantistici, quindi creeremo l’architettura della rete neurale. Infine, la utilizzeremo per calcolare l’energia di stato fondamentale dell’idrogeno molecolare (H₂) a varie distanze interatomiche. Alla fine di questo blog, imparerete a implementare le reti neurali per calcolare le energie di stato fondamentale, a ottimizzare i parametri di un PQC per un particolare costo dell’hamiltoniana e a osservare come l’uso di una rete neurale sia paragonabile all’uso di PQC senza misurazione a metà circuito.
Nota dell’editore: anche se abbiamo cercato di semplificare il più possibile il linguaggio di questo blog, esso presuppone comunque una conoscenza pratica delle reti neurali e dell’informatica quantistica. Per iniziare a conoscere entrambi gli argomenti, fate riferimento alla Qiskit Global Summer School dell’anno scorso, che si è concentrata sul Quantum Machine Learning.
Introduzione
Le reti neurali classiche comprendono due parti: neuroni artificiali costruiti da componenti lineari e funzioni di attivazione non lineari aggiunte successivamente. Xia e Kais immaginano invece una rete neurale ibrida quantistico-classica, in cui un PQC sostituisce i neuroni artificiali come componente lineare, mentre le misure – i valori di aspettativa degli operatori Pauli-Z su ciascun qubit – fungono da elemento classico e da funzione di attivazione non lineare che collega le componenti quantistiche. Iniziamo codificando la lunghezza del legame di una molecola nel nostro circuito, quindi aggiungiamo porte parametrizzate. Dopo ogni strato, eseguiamo la misurazione e utilizziamo i valori di aspettativa per inizializzare lo strato successivo della nostra rete neurale.
Questa struttura può sembrare simile ad altri algoritmi quantistici variazionali, in cui i parametri vengono aggiornati per minimizzare il valore di aspettativa. Tuttavia, le reti neurali sono leggermente diverse: sono più flessibili e non è necessario ottimizzare per ogni caso specifico. Una volta addestrato il nostro sistema, possiamo usarlo per fare previsioni per altri casi.
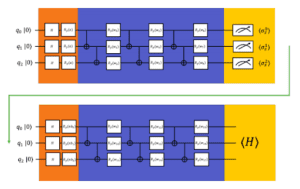
Nell’immagine precedente, la parte blu è il PQC, la parte arancione in alto rappresenta la codifica della lunghezza del legame e la parte gialla in alto è quella in cui si calcolano i valori di aspettativa b_i dell’operatore Pauli z per ogni qubit:
![]()
Dopo la misurazione, ripetiamo questo passaggio e reinseriamo i valori di aspettativa nel circuito. Una volta terminata questa iterazione, passiamo alla fase gialla inferiore: calcoliamo l’energia dello stato fondamentale, rappresentata dal valore di aspettativa dell’hamiltoniana.
Generiamo i dati di addestramento e di test da una serie di valori calcolati utilizzando un Eigensolver classico per minimizzare i valori di aspettativa dello stato fondamentale:
![]()
Implementazione del circuito quantistico
Inizieremo caricando le librerie Qiskit necessarie, mostrate nel gist GitHub qui sotto. Se siete alle prime armi con l’informatica quantistica, date un’occhiata al libro di testo di Qiskit. Potete trovare ulteriori informazioni e codificare il vostro primo circuito qui.
Codifica
Il primo passo consiste nel codificare i dati classici in uno stato quantistico per creare l’input. Nel nostro caso particolare siamo interessati a usare la codifica variazionale per codificare la lunghezza del legame in uno stato quantistico, dove usiamo un input per preparare le porte quantistiche e i loro parametri. L’idea è essenzialmente quella di mappare i dati classici in uno spazio di Hilbert utilizzando una mappa di caratteristiche, come in una rete neurale classica. Maggiori informazioni sulla codifica dei dati sono disponibili in questa lezione. Utilizzando la codifica variazionale, qualsiasi serie di dati può essere rappresentata come:
![]()
Dove:

Ry is a rotation around the y axis by an angle inputted as a parameter and H is the Hadamard gate.
Allora la codifica può essere scritta matematicamente come
![]()
O, più semplicemente, a ogni qubit di stato fondamentale applichiamo un gate di Hadamard e una rotazione parametrizzata intorno all’asse y, dove ogni punto di dati sulla lunghezza del legame viene convertito nel parametro per Ry.
Circuito quantistico parametrizzato
Il PQC è il nucleo della rete neurale – la parte blu della prima immagine – creato utilizzando i gate Ry e CNOT, come nel gist sottostante. Si possono vedere i parametri codificati nel circuito come parametri che saranno ottimizzati con un ottimizzatore classico. Come promemoria, le routine che coinvolgono circuiti quantistici parametrizzati iniziano con un’ansatz, o una prima ipotesi, che viene poi ottimizzata attraverso ripetute iterazioni del circuito.
Questi parametri vengono utilizzati per produrre lo stato variazionale |ψ(θ)>, che useremo insieme all’hamiltoniana della molecola per calcolare il valore di aspettativa e ottenere l’energia della molecola. Questi parametri saranno determinati in seguito, addestrando il nostro circuito sui valori esatti che troveremo con i consueti metodi della chimica quantistica.
Circuito di rete neurale
Quindi, dobbiamo calcolare i valori di aspettativa. Questo si può ottenere calcolando la probabilità di ottenere ciascuno degli stati base. Il nostro esempio è una rete neurale a due strati: questa profondità è più che sufficiente per ottenere valori approssimativi dello stato fondamentale della molecola. Per creare il circuito della rete neurale combineremo le due funzioni create in precedenza, encode e apply_ansatz, quindi calcoleremo il valore di aspettativa dell’operatore Pauli Z per ogni qubit dopo ogni strato. Dopo ogni strato utilizziamo il comando qc.reset() per inizializzare lo strato successivo del circuito. Alla fine di tutti gli strati calcoliamo l’energia.
Il circuito della rete neurale per alcuni parametri casuali è riportato di seguito
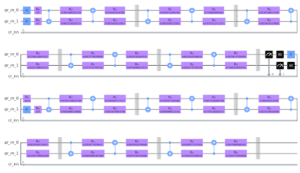
I dati
La parte successiva consiste nell’ottenere i dati di training e di test per addestrare ed eseguire la nostra rete neurale. Qui calcoliamo l’energia di stato fondamentale dell’idrogeno molecolare a varie distanze interatomiche. Per ciascuna di queste distanze, dobbiamo creare un driver per la molecola da una libreria di chimica computazionale. Questo driver può essere utilizzato per ottenere l’hamiltoniana e fornire ulteriori informazioni sulla molecola.
Di seguito sono riportate le soluzioni esatte ottenute con un Eigensolver classico.
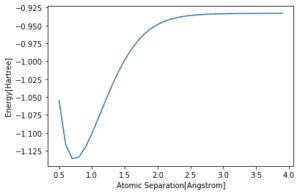
Dati di addestramento e di test
Dividiamo i dati in dati di addestramento e dati di test in modo casuale. I dati di addestramento saranno utilizzati per ottenere i parametri ottimizzati del nostro circuito.
Hamiltoniano
L’operatore di qubit può essere ottenuto utilizzando Qiskit Nature. Convertiamo l’hamiltoniana fermionica della molecola data in un operatore Qubit utilizzando un mapper. In questa esercitazione abbiamo utilizzato il Parity Mapper. La funzione definita di seguito restituisce un Operatore Qubit che varia con la lunghezza del legame di una molecola di idrogeno.
Energia
Infine, usiamo il simulatore di vettori di stato per ottenere il vettore di stato e poi usiamo la moltiplicazione matriciale per ottenere il valore di aspettativa. Questo metodo è fattibile solo su un simulatore e per ottenere i valori di aspettativa su un computer quantistico è necessario utilizzare metodi più elaborati. L’idea di base è quella di decomporre l’operatore hamiltoniano di Qubit in operatori di Pauli e quindi utilizzare un test di Hadamard per ottenere i valori di aspettativa di questi operatori di Pauli separatamente. I test di Hadamard non possono essere utilizzati direttamente perché l’operatore Qubit ottenuto non è unitario.
Nota – Qiskit fornisce anche un metodo per calcolare il valore di aspettativa utilizzando StateFn(), ma questo richiede che nel nostro circuito ci siano solo bit quantistici e questo non è possibile poiché abbiamo introdotto la non linearità basata sui bit classici.
Formazione
Faremo un apprendimento non supervisionato minimizzando il valore di aspettativa per ogni caso, usando la funzione Minimize di Scipy. In questa funzione si deve passare come argomento una funzione obiettivo con i parametri che devono essere ottimizzati, definendo il costo. Di seguito definiamo questa funzione obiettivo.
Siate pazienti con i comandi che seguono, poiché l’ottimizzazione classica richiede un certo tempo. Inoltre, l’esecuzione dei comandi potrebbe produrre parametri diversi, alcuni dei quali potrebbero non produrre buone approssimazioni.
Ora abbiamo ottenuto i parametri ottimizzati. Con questi otterremo l’energia degli ingressi di prova.
Infine, tracciamo la curva per i dati di test e di addestramento e osserviamo che questa è davvero vicina alla risposta reale.
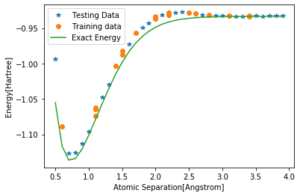
Senza non linearità
L’idea principale della misura intermedia è quella di introdurre la non linearità in uno spazio altrimenti lineare. Verifichiamo quindi cosa succede se eliminiamo la parte di misurazione.
L’intera procedura di addestramento, calcolo dei costi, ottimizzazione e test rimane la stessa di cui sopra.
Il circuito con parametri casuali può essere visto qui sotto. Tutto rimane invariato, ma viene eliminata la parte intermedia di misurazione e reinizializzazione.
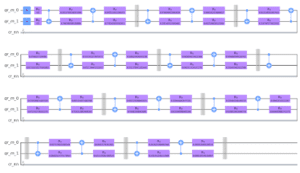
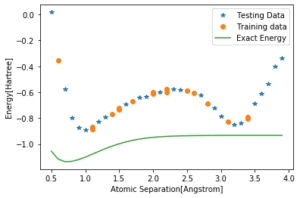
Osserviamo che la curva per l’addestramento e il test non è affatto vicina all’energia esatta, il che dimostra che la nostra rete neurale è un notevole passo avanti rispetto ai circuiti quantistici parametrizzati. O, in altre parole, la non linearità introdotta dalla rete neurale di misurazione a metà circuito fornisce un evidente vantaggio rispetto ai circuiti quantistici solo parametrizzati.
I nostri prossimi passi sono esplorare diversi schemi di codifica dei dati per ottimizzare le risorse e studiare la fattibilità dell’implementazione su dispositivi reali, tenendo conto dell’influenza del rumore sui risultati.
Articolo originale di Daniel Sierra-Sosa
Share:


