Inizializzazione dei pesi
Articolo in lingua originale di Semih Gülüm

Inizializzazione dei pesi
Negli studi di machine learning e deep learning, lo scopo principale è quello di minimizzare la funzione di perdita. Per raggiungere il minimo il prima possibile, è necessario inizializzare i pesi in base al nostro caso. Questo problema è chiamato “inizializzazione dei pesi”. La prima cosa da sapere è che si tratta di una decisione da prendere in fase di progettazione. Prima di addestrare la rete, è necessario inizializzare tutti i pesi. I valori iniziali dei pesi possono avere un impatto significativo sul processo di addestramento. A seconda del punto da cui il modello di deep learning parte nel processo di addestramento, può convergere verso uno qualsiasi dei possibili minimi locali della superficie di perdita irregolare.
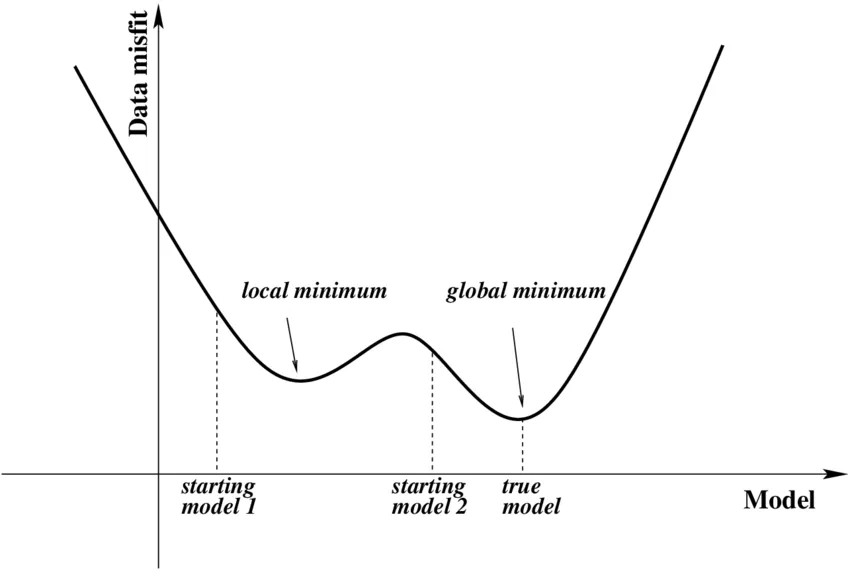
Riflettiamo insieme. Se iniziamo tutti i pesi da 0, sarà una scelta sbagliata sia in termini di tempo che di costi. Oppure ha senso farli partire tutti da 0.5? Iniziare con i pesi sbagliati porta a un gradiente che esplode o che svanisce durante la discesa del gradiente? La risposta è sì! Ecco perché abbiamo bisogno di un’inizializzazione.
Perchè ci serve inizializzare i pesi?
- Il risultato dell’addestramento di una rete neurale artificiale dipende dal setting iniziale dei pesi e dei bias
- La discesa del gradiente stocastico (SGD) converge ad un minimo locale
- Per evitare problemi di evanescenza o esplosione del gradiente. (Inizializzazioni tropp ograndi portano all’esplosione del gradiente, mentre inizializzazioni troppo piccole portano ad un gradiente che svanisce)
Tecniche di inizializzazione dei pesi
- Inizializzazione zero
- Inizializzazione random
- Inizializzazione Xavier
- Inizializzazione He-et-al
- Inizializzazione LeCun
Esaminiamo ciascuna di queste più nel dettaglio! Per semplificare il problema, fatemi usare un modello base per tutte le tecniche di inizializzazione.
model = tf.keras.models.Sequential([ tf.keras.layers.Flatten(input_shape=(64, 32)), tf.keras.layers.Dense(128, activation='relu', kernel_initializer, bias_initializer)])
1. Inizializzazione zero
Come suggerisce il nome, l’inizializzazione zero riguarda inizializzare tutti i pesi della rete neurale al valore 0. Questo viene fatto con l’assunzione che metà dei pesi finali sono positivi e l’altra metà negativi.
Se tutti i pesi nella rete vengono inizializzati a zero, tutte le attivazioni sono zero e di conseguenza anche i gradienti. In realtà, non importa nemmeno se i pesi sono inizializzati a qualsiasi altra costante. Le attivazioni potrebbero non essere zero in questo caso ma saranno comunque tutte uguali. Quindi possiamo escludere l’inizializzazione zero/costante.
model = tf.keras.models.Sequential([ tf.keras.layers.Flatten(input_shape=(64, 32)), tf.keras.layers.Dense(128, activation='relu', kernel_initializer='zeros', bias_initializer='zeros') ])
2. Inizializzazione random
Quando la funzione di attivazione è sigmoide, più il valore del peso è lontano da 0, più grande è la deviazione standard, più il valore di uscita è distorto vicino a 0 e 1, e quindi il gradiente viene perso. Un modo per risolvere questo problema è quello di inizializzare i pesi in una distribuzione normale con una piccola deviazione standard. In generale, i pesi iniziali sono inizializzati in modo casuale con una distribuzione normale (distribuzione gaussiana) con una media di 0 e una deviazione standard di 0,01 come segue
![]()
# With normal distributions model = tf.keras.models.Sequential([ tf.keras.layers.Flatten(input_shape=(64, 32)), tf.keras.layers.Dense(128, activation='relu', kernel_initializer='RandomNormal', bias_initializer='zeros') ]) ''' # With Uniform Distributions model = tf.keras.models.Sequential([ tf.keras.layers.Flatten(input_shape=(64, 32)), tf.keras.layers.Dense(128, activation='relu', kernel_initializer='RandomUniform', bias_initializer='zeros') '''
3. Inizializzazione Xavier (Glorot)
L’inizializzazione casuale si interrompe rapidamente per le reti profonde. Il motivo è che l’attivazione cade rapidamente a zero dopo pochi layer (e lo stesso vale per i gradienti). L’inizializzazione di Xavier mira a inizializzare i pesi in modo che la varianza di ogni layer sia la stessa. In altre parole, la varianza dell’uscita di ogni layer deve essere uguale alla varianza dell’ingresso e la varianza del gradiente prima e dopo il passaggio attraverso i layer nella backpropagation deve essere la stessa.
# With normal distributions model = tf.keras.models.Sequential([ tf.keras.layers.Flatten(input_shape=(64, 32)), tf.keras.layers.Dense(128, activation='relu', kernel_initializer='glorot_normal', bias_initializer='zeros') ]) ''' # With Uniform Distributions model = tf.keras.models.Sequential([ tf.keras.layers.Flatten(input_shape=(64, 32)), tf.keras.layers.Dense(128, activation='relu', kernel_initializer='glorot_uniform', bias_initializer='zeros') '''
4. Inizializzazione He-et-al
Kaiming He ha proposto un valore iniziale adeguato per la ReLU che viene chiamato valore iniziale di He. Questo tipo di inizializzazione è simile a quella di Xavier ma non identica. Le differenze sono dovute alla non-linearità della funzione di attivazione ReLU e utilizzano diversi fattori di scala per i pesi.
# With normal distributions model = tf.keras.models.Sequential([ tf.keras.layers.Flatten(input_shape=(64, 32)), tf.keras.layers.Dense(128, activation='relu', kernel_initializer='he_normal', bias_initializer='zeros') ]) ''' # With Uniform Distributions model = tf.keras.models.Sequential([ tf.keras.layers.Flatten(input_shape=(64, 32)), tf.keras.layers.Dense(128, activation='relu', kernel_initializer='he_uniform', bias_initializer='zeros') '''
5. Inizializzazione LeCun
E’ anche conosciuta come “efficient backprop”, considera la dimensione dell’input e dell’output di ciascun layer. Questo metodo può essere usato con funzioni di attivazione che non sono necessariamente simmetriche rispetto allo zero, come ad esempio la tangente iperbolica. Genera pesi che sono numeri selezionati casualmente e moltiplicati per la varianza 1/dimensioni_layer_input.
# With normal distributions model = tf.keras.models.Sequential([ tf.keras.layers.Flatten(input_shape=(64, 32)), tf.keras.layers.Dense(128, activation='relu', kernel_initializer='lecun_normal', bias_initializer='zeros') ]) ''' # With Uniform Distributions model = tf.keras.models.Sequential([ tf.keras.layers.Flatten(input_shape=(64, 32)), tf.keras.layers.Dense(128, activation='relu', kernel_initializer='lecun_uniform', bias_initializer='zeros') '''
Interrogativi
Come si può capire che un’inizializzazione è valida?
- Porta a perdite più piccole sui set di training e di test
- Non satura la maggior parte delle unità sigmoidi o tangenti iperboliche
- Non esplode con le unità ReLU
- Il valore del gradiente è simile tra i vari layer
Come trovare valori di inizializzazione appropriati?
- La media della attivazioni dovrebbe essere zero
- La varianza delle attivazioni dovrebbe rimanere la stessa tra i vari layer
Reference
- https://sebastianraschka.com/pdf/lecture-notes/stat453ss21/L11_norm-and-init__slides.pdf
- https://machinelearningmastery.com/weight-initialization-for-deep-learning-neural-networks/#:~:text=Weight%20initialization%20is%20a%20procedure,of%20the%20neural%20network%20model.
- https://heartbeat.comet.ml/weight-initialization-in-deep-neural-networks-e7e0d526f900
- https://wandb.ai/sauravmaheshkar/initialization/reports/A-Gentle-Introduction-To-Weight-Initialization-for-Neural-Networks–Vmlldzo2ODExMTg
- https://medium.com/guidona-softpedia/weight-initialization-methods-in-neural-networks-a3e7a793cee5
- https://machinelearningmastery.com/weight-initialization-for-deep-learning-neural-networks/#:~:text=Weight%20initialization%20is%20a%20procedure,of%20the%20neural%20network%20model.
- https://koreascience.kr/article/JAKO201909055503906.pdf
- https://web.eecs.umich.edu/~justincj/slides/eecs498/498_FA2019_lecture10.pdf
- https://sebastianraschka.com/pdf/lecture-notes/stat453ss21/L11_norm-and-init__slides.pdf
- https://bigmeca.minesparis.psl.eu/wp-content/uploads/2021/02/neural_networks2_handouts.pdf
- https://www.deeplearning.ai/ai-notes/initialization/index.html
- https://www.tensorflow.org/api_docs/python/tf/keras/initializers
Share:


