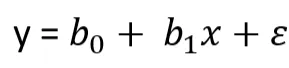La regressione logistica è sufficiente?

Articolo in lingua originale di Amruthabnair

“La regressione logistica è un esempio di apprendimento supervisionato. In questo articolo vi accompagneremo in un viaggio emozionante nel regno della regressione logistica, dove imparerete cos’è, esaminerete i suoi tipi di base, la confronterete con la regressione lineare, ne valuterete i vantaggi e gli svantaggi e conoscerete le sue applicazioni reali. Preparatevi a sbloccare la potenza della regressione logistica e a intraprendere un viaggio emozionante alla scoperta dei dati!”.

Cosa è la regressione logistica?

Quando la variabile da prevedere è continua, ma deve essere classificata in forma binaria, si ricorre alla Regressione logistica. Questo apprendimento supervisionato viene utilizzato per calcolare o prevedere la probabilità binaria (eventi che si verificano sì o no).

Ad esempio: febbre o no, cancro o no, guadagno o perdita, promozione o bocciatura. L’obiettivo della regressione logistica è quello di trovare la relazione tra le variabili indipendenti e le variabili dipendenti binarie che assumono il valore di 0 o 1.

Rappresentazione grafica della regressione logistica

Regressione lineare vs. regressione logistica

Sia la Regressione lineare che quella logistica sono modelli statistici, ma presentano alcune caratteristiche fondamentali.

Innanzitutto, vediamo cosa sono la Regressione lineare e la Regressione logistica.

Regressione lineare

La regressione lineare viene utilizzata per modellare una relazione tra variabili dipendenti e indipendenti continue. L’output di questa variabile può essere qualsiasi valore. In sostanza, lo scopo di questo modello è determinare l’equazione lineare più adatta a rappresentare la relazione tra la variabile indipendente e la variabile dipendente.

L’espressione matematica della regressione lineare è:

Dove:

y è la variabile dipendente, il valore da predire
x è la variabile indipendente, la variabile utilizzata per la previsione
b0 è l’intercetta e b1 la pendenza
e è l’errore residuo, ovvero la distanza tra la linea ottenuta dalla funzione e il punto reale. L’errore può essere positivo o negativo

Rappresentazione grafica

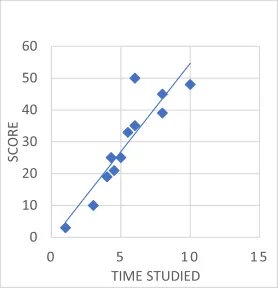
Regressione logistica

Nella Regressione Logistica, invece di applicare una linea, si utilizza una curva chiamata Curva Sigmoide. Nella fig: 1.2, la curva a forma di S è la curva sigmoide, nota anche come funzione sigmoide o funzione logistica, che mappa qualsiasi numero di valore reale con una probabilità compresa tra 0 e 1. La funzione di massima verosimiglianza per la stima dei parametri è il metodo più comunemente utilizzato nella regressione logistica.

La funzione di massima verosimiglianza per la stima dei parametri è il metodo più comunemente utilizzato nella regressione logistica. Trovare i valori dei coefficienti che massimizzano la verosimiglianza dei dati osservati è l’obiettivo principale di questo metodo di stima. Durante il processo di addestramento, il modello di regressione logistica apprende i coefficienti delle variabili indipendenti che massimizzano la probabilità degli esiti binari osservati nei dati di addestramento. Dopo che il modello è stato addestrato utilizzando il MLE, la soglia viene applicata per prevedere le probabilità per ottenere la classificazione binaria. Poiché il valore di soglia è impostato per default su 0,5, qualsiasi valore di probabilità superiore a 0,5 è considerato positivo e qualsiasi valore inferiore a 0,5 è considerato negativo. Tuttavia, il valore di soglia può essere regolato in base a un problema specifico.

La rappresentazione matematica della regressione logistica è che:

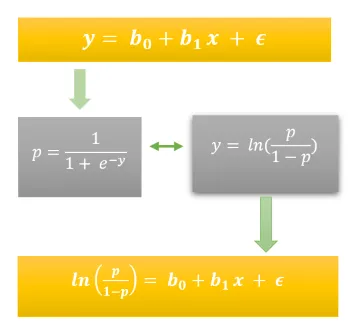
Fig.1.4. Rappresentazione matematica della regressione logistica (immagine dell’autore)

La Figura 1.4 mostra come abbiamo derivato la regressione logistica dall’equazione lineare. Cioè sostituendo il valore della funzione sigmoide in termini di y nell’equazione della retta.

Le differenze principali tra la regressione logistica e le regressioni lineari sono:

La regressione lineare viene utilizzata per gestire problemi di regressione che prevedono la previsione di un valore numerico continuo come output, mentre la regressione logistica viene utilizzata per gestire problemi di classificazione che prevedono la previsione di categorie o classi discrete come output.
La regressione lineare richiede una relazione tra una variabile dipendente e una indipendente e questa relazione può essere rappresentata da una linea retta, mentre la regressione logistica non richiede questo tipo di relazione. Utilizza invece la probabilità dei dati mediante una funzione logistica (funzione sigmoide).
Partendo dal presupposto che tutte le altre variabili sono costanti, i coefficienti di regressione lineare indicano come una variazione di un’unità delle variabili predittive avrà un impatto sui risultati. D’altro canto, i coefficienti della regressione logistica, presupponendo che tutte le altre variabili rimangano costanti, mostrano la variazione del log-odds dell’esito binario associato a una variazione di un’unità della variabile predittiva. (Il log-odds è il logaritmo naturale delle probabilità, ovvero il rapporto tra la probabilità che il risultato binario si verifichi e la probabilità che non si verifichi.
Ad esempio: Nel caso della previsione del superamento o meno di un esame da parte di uno studente, nella regressione lineare (fig. 1.2), possiamo inserire una retta lineare rispetto alle variabili indipendenti, come l’ora in cui lo studente ha studiato. Tuttavia, la regressione lineare potrebbe non essere ideale per questo caso, in quanto non è in grado di prevedere con esattezza se uno studente supera o meno l’esame. Infatti, quando si applica un’equazione lineare in questo caso, l’output sarà pass/fail =, dove x è l’ora studiata, sono il coefficiente. Il valore di uscita non sarà compreso tra 0 e 1. D’altra parte, nel caso della regressione logistica, figura 1.1, possiamo modellare la probabilità che uno studente superi o meno l’esame utilizzando la funzione sigmoide. Per massimizzare la possibilità di individuare l’output reale, il modello di regressione logistica stima i coefficienti (0 e 1). Utilizzando un numero soglia, la probabilità prevista può essere utilizzata per classificare lo studente come promosso o bocciato. (ad esempio, 0,5).

Fig.1.5. Regressione logistica vs. regressione lineare (sorgente: Java_T point)

Tipi di regressione logistica

Esistono principalmente tre tipi di regressione logistica:

Regressione logistica binaria: La regressione logistica è la relazione tra le variabili indipendenti e quelle dipendenti. In questo caso la variabile dipendente è binaria, ossia può assumere solo due valori possibili, 0 o 1. Ad esempio, se una persona acquista o meno un prodotto, se una persona passa o non passa l’esame, se è un giorno di pioggia o meno.
Regressione logistica multinomiale:La regressione logistica multinomiale è un modello statistico utilizzato per modellare la relazione tra le variabili dipendenti e due o più variabili indipendenti. In questo caso, le variabili dipendenti sono categoriali e possono essere due o più e non ordinate. Ad esempio, malattie mediche come (malattia A, malattia B, malattia C), animali (cani, gatti, pecore, topi).
Regressione logistica ordinale: È un modello statistico utilizzato per modellare la relazione tra variabili dipendenti ordinali e due o più variabili indipendenti. In questo caso la variabile dipendente è ordinale, cioè ordinata, ad esempio il voto degli studenti (eccellente, buono, medio, sotto la media, scarso) o lo stato di salute (critico, grave, lieve, sano).

Pro e contro della regressione logistica

Vantaggi

Può essere facilmente applicata quando i dati possono essere separati linearmente
Ha una grande abilità di estensione a classi multiple come nei casi della regressione logistica multinomiale e di quella ordinale
Può classificare record sconosciuti in modo rapido
Ha buone performance per molti dataset semplici e una buona accuratezza quando il dataset può essere separato linearmente
Visto che aggiornare la regressione logistica è semplice, ogni volta che aggiungiamo dati al dataset esistente, questo aiuta a migliorare accuratezza e utilità del modello nel tempo.
A causa delle abilità di processing efficaci, può gestire datasets enormi, Questo lo rende uno strumento efficace per studiare problemi di classificazione binaria con grandi quantità di dati.

Svantaggi

Lo svantaggio principale della regressione logistica è l’assunzione di linearità tra la variabile dipendente e la variabile indipendente. Pertanto, questa regressione potrebbe non essere il modello migliore da utilizzare per problemi in cui la relazione tra le variabili è complessa o la regressione logistica richiede una multicollinearità media o nulla tra le variabili indipendenti.
Esiste un’alta probabilità che il modello venga overfittato. Per essere precisi, nella regressione logistica, quando i dati contengono numerose variabili indipendenti, il modello può cercare di adattarsi al rumore presente nei dati, con conseguenti basse prestazioni di generalizzazione. Allo stesso modo, quando la dimensione del campione è troppo piccola, potrebbero non esserci abbastanza dati da stimare e il modello potrebbe essere sovradimensionato.
Le relazioni complesse sono difficili da ottenere con la regressione logistica.
La regressione logistica richiede un campione di grandi dimensioni, in modo da poter produrre stime accurate del coefficiente. Al contrario, il modello non è in grado di effettuare stime accurate quando la dimensione del campione di dati è minima.
La regressione logistica è limitata alla classificazione binaria ed è stata progettata principalmente per risolvere questo tipo di problemi di classificazione, cioè quando i valori della variabile dipendente possono essere 0 o 1, oppure “sì” o “no”. Tuttavia, è possibile utilizzare anche problemi con più di due esiti, come la classificazione multinomiale.
La regressione logistica è sensibile agli outlier. La regressione logistica può essere sensibile agli outlier nei dati, che possono influenzare le stime dei coefficienti e le prestazioni complessive del modello.

Applicazioni della regressione logistica

Esistono diverse applicazioni reali della regressione logistica, in particolare quando si cerca di prevedere risultati binari.

Campo medico: la regressione logistica può essere utilizzata per prevedere la malattia di un paziente in base alla sua storia clinica e ad altri fattori di rischio. Inoltre, può essere utilizzata per l’identificazione dei fattori di rischio, lo studio dei risultati delle terapie e altro ancora.
Credit scoring: Nelle banche e in altre istituzioni finanziarie, il modello di punteggio di credito basato sulla regressione logistica è il più utilizzato per convalidare la valutazione del rischio di credito. In questo caso, la capacità del mutuatario di rimborsare il prestito è la variabile dipendente, mentre una serie di altre caratteristiche, come il reddito e la situazione lavorativa del mutuatario, sono le variabili indipendenti.
Previsioni politiche: La regressione logistica può essere utilizzata per prevedere l’esito delle elezioni. La variabile dipendente è la vittoria o meno di un determinato candidato, mentre la variabile indipendente è il comportamento dell’elettore, le opinioni politiche. Per prevedere i risultati delle elezioni, le società di sondaggi e i media utilizzano spesso modelli di previsione politica basati sulla regressione logistica.
Rilevamento delle frodi: L’obiettivo principale è scoprire dove si è verificato un comportamento fraudolento in base alle caratteristiche di input.
Gioco d’azzardo: La segmentazione dei giocatori e il loro abbandono possono essere previsti utilizzando la regressione logistica, analizzando il comportamento dei giocatori, come la frequenza di gioco, il tipo di gioco e gli acquisti in-game.

Conclusione

In conclusione, l’apprendimento supervisionato è un argomento essenziale del machine learning che comprende sia i modelli di classificazione sia quelli di regressione. Qui ho discusso la regressione logistica, che appartiene all’algoritmo di classificazione. Questa regressione viene utilizzata quando la variabile dipendente è di tipo categorico. Anche se presenta diverse limitazioni, come la sensibilità ai contorni e l’alta probabilità di overfitting, è ampiamente utilizzata in problemi del mondo reale, come nel campo medico, nel credit scoring, nelle previsioni politiche e nella dizione delle frodi.

Spero che vi sia piaciuto!