Massima verosimiglianza vs. Stima Bayesiana
Un confronto tra metodi di stima dei parametri
Articolo in lingua originale di Lulu Ricketts
Il machine learning si basa essenzialmente sui modelli. Come possiamo rappresentare i dati? In che modi possiamo raggruppare i dati per fare dei confronti? Da quale distribuzione o modello provengono i nostri dati? Queste domande (e molte molte altre) guidano i processi dei dati, ma quest’ultima è la base della stima dei parametri.
La stima della massima verosimiglianza (MLE), la visione frequentista, e la stima bayesiana, la visione bayesiana, sono forse i due metodi più utilizzati per la stima dei parametri: il processo attraverso il quale, dati alcuni dati, siamo in grado di stimare il modello che li ha generati. Perché è importante? I dati raccolti nel mondo reale non sono quasi mai rappresentativi dell’intera popolazione (immaginate quanti ne dovremmo raccoglierne!) e quindi, stimando i parametri della distribuzione da un campione di popolazione osservato, possiamo ottenere informazioni su dati che non vengono osservati.
Come prerequisito di questo articolo, è importante che abbiate prima compreso i concetti di calcolo e teoria della probabilità, tra cui la probabilità congiunta e condizionata, le variabili casuali e le funzioni di densità di probabilità.
La stima dei parametri ha a che fare con l’approssimazione dei parametri di una distribuzione, il che significa che il tipo di distribuzione è tipicamente assunto in anticipo, il che determina quali sono i parametri sconosciuti da stimare (λ per Poisson, μ e σ² per una distribuzione Gaussiana). L’esempio che utilizzerò in questo articolo sarà quello della Gaussiana.
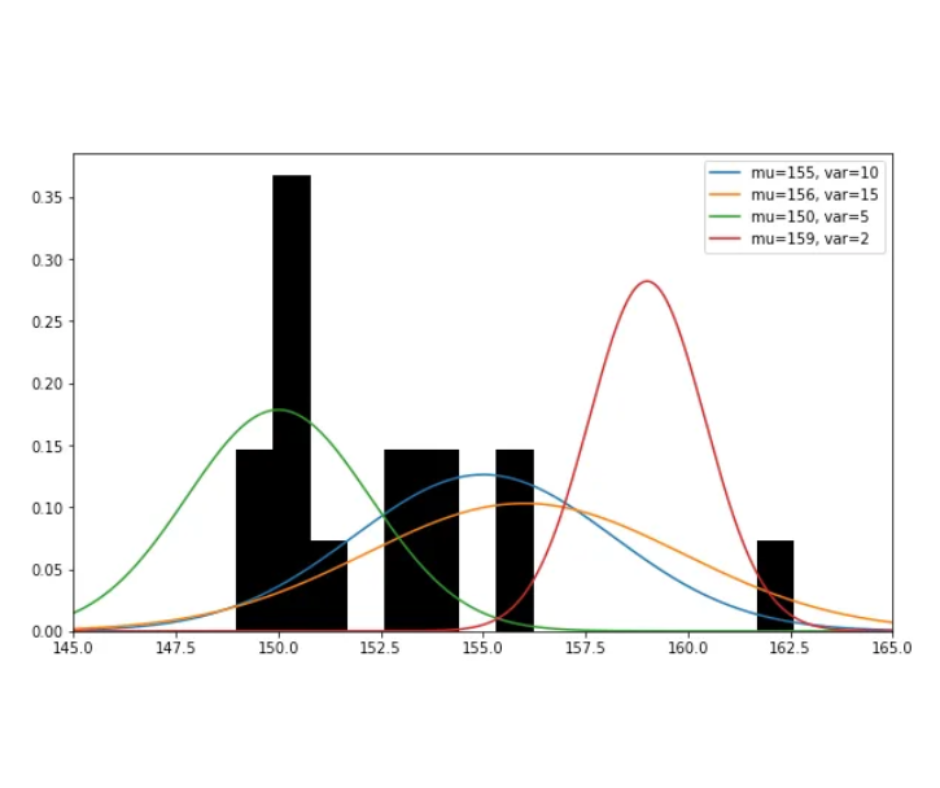
Esempio: supponiamo di voler conoscere la distribuzione dell’altezza degli alberi di una foresta come parte di uno studio ecologico longitudinale sulla salute degli alberi, tuttavia gli unici dati a noi disponibili per l’anno corrente sono relativi ad un campione di 15 alberi, registrato da un escursionista. La domanda a cui vorremmo rispondere è: con quale distribuzione possiamo modellare l’altezza degli alberi dell’intera foresta?

Breve nota sulla notazione
θ sono le variabili non note, nel caso di una distribuzione Gaussiana θ = (μ,σ²)
D sono tutti i dati osservati, D = (x_1, x_2,…,x_n)
Funzione di verosimiglianza
Pressoché l’unico punto in comune tra stima MLE e stima Bayesiana riguarda la loro dipendenza dalla verosimiglianza dei dati osservati (nel caso d’esempio i 15 alberi). La verosimiglianza descrive la possibilità che ha ciascun valore di ogni parametro di aver generato i dati osservati ed è data da:

Grazie alla fantastica assunzione i.i.d. (indipendenti ed identicamente distribuiti) tutti i dati vengono considerati indipendenti, possiamo quindi dimenticare le confuse probabilità condizionate.
Torniamo al nostro problema. Conoscendo i valori dei nostri 15 campioni, qual è la probabilità di ogni combinazione di parametri non-noti (μ,σ²) di aver prodotto questo insieme di dati?
Utilizzando la funzione di distribuzione gaussiana, la nostra funzione di verosimiglianza è:

Stima della massima verosimiglianza (MLE)
Fantastico. Ora che conoscete la funzione di verosimiglianza, calcolare la massima verosimiglianza è davvero facile. La risposta è già nel nome. Per ottenere i nostri parametri stimati (𝜃̂), tutto ciò che dobbiamo fare è trovare i parametri che producono la massima verosimiglianza. In altre parole. la combinazione di (μ,σ²) che permette di ottenere il punto più chiaro (giallo) in cima alla funzione di verosimiglianza rappresentata nell’immagine sopra.
Per trovare questo valore, dobbiamo applicare un po’ di calcolo e di derivate:

Come avrete notato, c’è un problema. Considerare le derivate di prodotti può diventare davvero complesso e vogliamo evitarlo. Fortunatamente c’è un modo per aggirare il problema: utilizzare la funzione di verosimiglianza in versione logaritmica. Ricordiamo che
- Il logaritmo di un prodotto corrisponde alla somma tra i logaritmi dei fattori
- Considerare il logaritmo di qualsiasi funzione può cambiarne i valori, ma non cambia il punto in cui si verifica il massimo. Quindi otterremo la stessa soluzione.

Si scopre che per una variabile casuale gaussiana, la soluzione MLE è semplicemente la media e la varianza dei dati osservati. Quindi, per il nostro problema, la soluzione MLE che modella la distribuzione delle altezze degli alberi è una distribuzione gaussiana con μ=152,62 e σ²=11,27.
Stima Bayesiana
Buone notizie! Un aiuto alla nostra ricerca della distribuzione dell’altezza degli alberi nella foresta, un collega è riuscito ad accedere ai dati negli archivi e trovare l’altezza media degli alberi per gli scorsi 10 anni. Con questa informazione, possiamo utilizzare la stima Bayesiana per risolvere il problema.
L’idea centrale dietro alla stima Bayesiana è che prima di aver visto qualsiasi dato, abbiamo già qualche informazione a priori della distribuzione da cui proviene. Questa conoscenza solitamente deriva dall’esperienza o da esperimenti passati. Prima di entrare nel vivo della questione, tuttavia, è essenziale comprendere il concetto del teorema di Bayes.
Teorema di Bayes
Si spera che conosciate, o che almeno abbiate ne sentito parlare, del Teorema di Bayes in un contesto probabilistico, in cui si vuole trovare la probabilità di un evento condizionato a un altro evento. In questa sede, spero di inquadrarlo in un modo che dia un’idea della stima bayesiana dei parametri e del significato degli antecedenti.

Per illustrare questa equazione, si consideri l’esempio in cui l’evento A = “oggi ha piovuto prima” e l’evento B = “l’erba è bagnata” e si voglia calcolare P(A|B), la probabilità che abbia piovuto prima dato che l’erba è bagnata. Per farlo, dobbiamo calcolare P(B|A), P(B) e P(A). La probabilità condizionale P(B|A) rappresenta la probabilità che l’erba sia bagnata dato che ha piovuto. In altre parole, è la verosimiglianza che l’erba sia bagnata, dato che è piovuto.
Il valore di P(A) è noto come antecedente: la probabilità che abbia piovuto indipendentemente dal fatto che l’erba sia bagnata o meno (prima di conoscere lo stato dell’erba). Questa conoscenza preventiva è fondamentale perché determina quanto peso diamo alla verosimiglianza. Se siamo in un luogo in cui non piove spesso, saremo più inclini ad attribuire il fatto che l’erba è bagnata a qualcos’altro che non sia la pioggia come rugiada o spruzzi, il che è catturato da un basso valore di P(A).
Se, invece, ci troviamo in un luogo in cui piove costantemente, è più probabile che l’erba sia bagnata a causa della pioggia, un valore elevato di P(A) riflette questa condizione.
Ciò che rimane è P(B), anche nota come l’evidenza: la probabilità che l’erba sia bagnata, evento che agisce come prova del fatto che abbia piovuto. Una proprietà importante di questo valore è che è una costante di normalizzazione per la probabilità finale e, come vedrete a breve, nella stima Bayesiana, si sostituisce un fattore di normalizzazione al posto della tradizionale “evidenza”.
L’equazione utilizzata per la stima bayesiana assume la stessa forma del teorema di Bayes, con la differenza che ora si utilizzano modelli e funzioni di densità di probabilità (pdf) al posto delle probabilità numeriche.

Si noti che, in primo luogo, la verosimiglianza è equivalente alla verosimiglianza utilizzata nel MLE e, in secondo luogo, l’evidenza tipicamente utilizzata nel Teorema di Bayes (che in questo caso si tradurrebbe in P(D)), è sostituita da un integrale del numeratore.
Questo perchè
- P(D) è estremamente difficile da calcolare
- P(D) non si basa su θ, che è ciò che ci interessa davvero
- La sua utilizzabilità come fattore di normalizzazione può essere sostituita con il valore integrale, che assicura che l’integrale della distribuzione a posteriori sia 1
Ricordiamo che per ottenere la soluzione numerica dei parametri (μ,σ²) nel caso del MLE, consideriamo l’argmax della funzione di verosimiglianza logaritmica. Nella stima Bayesiana, invece, calcoliamo una distribuzione sullo spazio dei parametri chiamata pdf a posteriori, indicata come p(θ|D). Questa distribuzione rappresenta quanto peso diamo ad ogni parametro per essere quello che può aver generato i nostri dati, dopo aver preso in considerazione sia i dati osservati che la conoscenza a priori.
Anche l’antecedente p(θ), è una distribuzione, di solito dello stesso tipo della distribuzione a posteriori. Non entrerò nei dettagli, tuttavia quando la distribuzione dell’antecedente coincide con quella a posteriori è noto come antecedente coniugato e permette svariati vantaggi dal punto di vista computazionale. Nel nostro esempio useremo gli antecedenti coniugati.
Torniamo ancora una volta al problema dell’altezza degli alberi. Oltre ai 15 alberi registrati dall’escursionista, ora abbiamo le medie delle altezze degli alberi negli ultimi 10 anni.

Partendo dal presupposto che quest’anno l’altezza degli alberi dovrebbe rientrare nella distribuzione di tutti gli anni precedenti, il nostro antecedente è la distribuzione gaussiana con μ=159,2 e σ²=9,3.
Non resta che calcolare la nostra pdf a posteriori. Per questo calcolo, assumo un σ² = σ²_MLE = 11,27. In realtà non risolveremmo la stima Bayesiana in questo modo, ma moltiplicando Gaussiane di dimensioni diverse, come la verosimiglianza e l’antecedente, è estremamente complicato e credo che semplificare i calcoli in questo caso è sufficiente per capire il processo ed è più facile da visualizzare. Se desiderate ulteriori risorse su come eseguire il calcolo completo, consultate questi due link.
Moltiplicando la verosimiglianza univariata e l’antecedente e normalizzando il risultato, si ottiene una distribuzione gaussiana posteriore con μ=155,85 e σ²=7,05.

Ed ecco il risultato della stima Bayesiana. Come si può notare, la distribuzione a posteriori tiene conto sia dell’antecedente che della verosimiglianza cercando un punto di incontro tra le due. Alla luce dei nuovi dati osservati, la componente a posteriori attuale diventa il nuovo antecedente e con la probabilità dei nuovi dati viene calcolata una nuova componente a posteriori.
Predizioni
Abbiamo modelli per descrivere i nostri dati, quindi cosa possiamo farci? L’uso principale di questi modelli è quello di fare previsioni su dati futuri non ancora osservati, che ci dicono essenzialmente quanto è probabile che un’osservazione provenga da questa distribuzione. Non mi soffermerò esplicitamente sui calcoli per il nostro esempio, ma le formule sono riportate di seguito se volete provare da soli.
• Predizione MLE

Per calcolare la probabilità, le predizioni di massima verosimiglianza utilizzano quelle delle variabili latenti nella funzione di densità. Ad esempio, nel caso Gaussiano, per calcolare le previsioni utilizziamo la soluzione della massima verosimiglianza per (μ,σ²).
• Predizione Bayesiana

Come avrete probabilmente indovinato, le predizioni Bayesiane sono un po’ più complicate, per ottenere la previsione di un nuovo campione utilizzano sia la distribuzione a posteriori che quella di una variabile randomica θ.
Osservazioni finali
Quando usare MLE e quanto la stima Bayesiana?
Abbiamo visto le differenze computazionali tra i due metodi di stima dei parametri, una domanda che ora sorge spontanea è: quando usare un metodo piuttosto che l’altro? Sebbene non ci sia una regola precisa per selezionare il metodo, spero che le domande che seguono possano essere utili come linee guida per orientarsi verso la scelta giusta:
- Con quanti dati si ha a che fare? MLE dipende unicamente dai dati osservati ed è noto per introdurre facilmente distorsioni se i dati sono pochi. Se consideriamo un esperimento in cui si lancia 3 volte una moneta non truccata e si ottiene sempre testa, nonostante sappiamo che la possibilità di avere testa è il 50%, calcolando la stima di massima verosimiglianza in questo caso otterremmo che la probabilità di avere testa, p(testa), è pari a 1, mentre quella di ottenere croce è 0. In situazioni in cui i dati osservati sono scarsi, incorporare la stima Bayesiana come conoscenza a priori può aiutare a raggiungere un modello più accurato, ad esempio conoscendo che una moneta non truccata ha 50% di probabilità di ottenere testa.
- Abbiamo conoscenze a priori affidabili riguardo al problema? Come appena detto, le conoscenze a priori possono migliorare il modello in alcune situazioni. Tuttavia se le conoscenze a priori non sono affidabili possono portare a modelli molto distorti che richiedono grandi quantità di dati osservati per essere corretti. Assicuratevi che state utilizzando componenti a priori ben definite e che contengano informazioni rilevanti al problema da risolvere. Se non siete sicuri dell’affidabilità delle conoscenze a priori, MLE può essere un’opzione migliore, soprattutto se disponete di una quantità sufficiente di dati.
- Avete risorse computazionali limitate? Un tema ricorrente in questo articolo è che i calcoli Bayesiani sono più complessi di quelli di MLE. Con il potere computazionale moderno questa differenza potrebbe essere di poco spessore, tuttavia se si hanno risorse limitate, MLE potrebbe essere la scelta adatta.
Alcune proprietà interessanti
Infine, avendo già discusso la maggior parte delle differenze tra MLE e stima Bayesiana, vorrei solamente lasciarvi alcuni collegamenti interessanti tra i due metodi:
- Se la conoscenza a priori di Bayes è uniforme per tutti i valori (non informativa), le previsioni Bayesiane potrebbero essere molto simili, se non uguali, a quelle MLE.
- Se la conoscenza a priori Bayesiana è ben definita e non zero in tutti i punti, allora, al crescere dei dati verso quantità infinite, le previsioni MLE e di Bayes convergono allo stesso valore.
Questo è tutto! Se siete arrivati fin qui, grazie per l’attenzione.
Share: