One Shot Learning con le reti siamesi utilizzando Keras

Introduzione

Articolo in lingua originale di Harshall Lamba

Le reti neurali convoluzionali profonde sono diventate lo stato dell’arte dei metodi di classificazione delle immagini. Tuttavia, una delle maggiori limitazioni è che richiedono una grande quantità di dati etichettati. In molte applicazioni, raccogliere una tale quantità di dati a volte non è fattibile. L’apprendimento One Shot mira a risolvere questo problema.

Prerequisiti

In questo post, si presuppone che abbiate già familiarità con le basi di machine learning e che abbiate un po’ di esperienza nell’uso delle reti neurali convoluzionali per la classificazione delle immagini utilizzando Python e Keras.

Classificazione vs. One Shot Learning

Nel caso della classificazione standard, l’immagine in ingresso viene usata come input ad una serie di layer e viene generata infine, all’uscita, una distribuzione di probabilità su tutte le classi (in genere utilizzando una Softmax). Ad esempio, se stiamo cercando di classificare un’immagine come gatto, cane, cavallo o elefante, allora per ogni immagine in ingresso generiamo 4 probabilità, che indicano la probabilità che l’immagine appartenga a ciascuna delle 4 classi. A questo punto è necessario notare due punti importanti. In primo luogo, durante il processo di addestramento, abbiamo bisogno di un gran numero di immagini per ciascuna delle classi (gatti, cani, cavalli ed elefanti). In secondo luogo, se la rete viene addestrata solo sulle 4 classi di immagini di cui sopra, non possiamo aspettarci di testarla su qualsiasi altra classe, ad esempio “zebra”. Se vogliamo che il nostro modello classifichi anche le immagini di zebre, allora dobbiamo prima ottenere molte immagini di zebre e poi dobbiamo riaddestrare il modello. Ci sono applicazioni in cui non abbiamo dati sufficienti per ogni classe e il numero totale di classi è enorme e cambia dinamicamente. Pertanto, il costo della raccolta dei dati e della riqualificazione periodica è troppo elevato.

D’altra parte, in una classificazione one shot, abbiamo bisogno di un solo esempio di addestramento per ogni classe. Sì, avete capito bene, solo uno. Da qui il nome One Shot. Cerchiamo di fare chiarezza con un esempio pratico del mondo reale.

Supponiamo di voler costruire un sistema di riconoscimento facciale per una piccola organizzazione con soli 10 dipendenti (i numeri piccoli semplificano le cose). Utilizzando un approccio di classificazione tradizionale, potremmo ottenere un sistema che si presenta come segue:

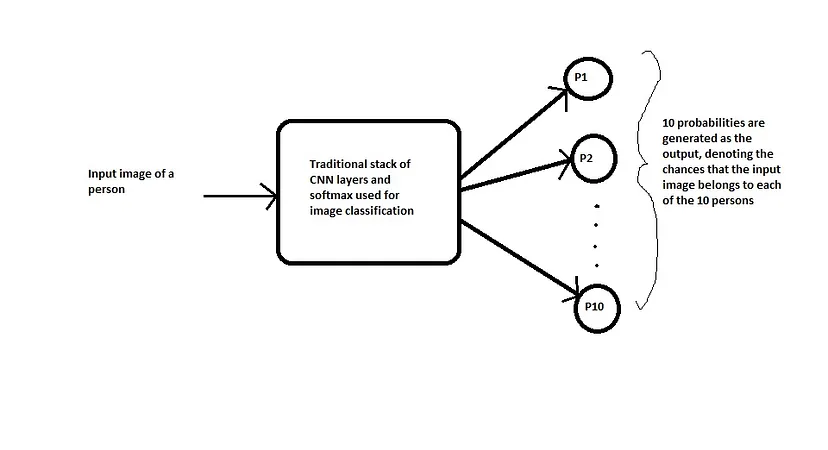
Problemi

Per addestrare un sistema di questo tipo, abbiamo bisogno di molte immagini diverse di ciascuna delle 10 persone dell’organizzazione, il che potrebbe non essere fattibile. (Immaginate di farlo per un’organizzazione con migliaia di dipendenti).
Cosa succede se una nuova persona entra o esce dall’organizzazione? È necessario raccogliere nuovamente i dati e addestrare nuovamente l’intero modello. Questo non è praticamente possibile, soprattutto per le grandi organizzazioni in cui le assunzioni e i licenziamenti avvengono quasi ogni settimana.

Vediamo ora come affrontare questo problema utilizzando la classificazione one shot, che aiuta a risolvere entrambi i problemi di cui sopra:

Invece di classificare direttamente un’immagine di input (test) come appartenente una delle 10 persone dell’organizzazione, questa rete prende in input un’immagine di riferimento extra della persona e produce un punteggio di somiglianza che indica la probabilità che le due immagini di input appartengano alla stessa persona. In genere, il punteggio di somiglianza viene schiacciato tra 0 e 1 utilizzando una funzione sigmoide, dove 0 indica nessuna somiglianza e 1 indica una somiglianza completa. Qualsiasi numero compreso tra 0 e 1 viene interpretato di conseguenza.

Si noti che questa rete non sta imparando a classificare un’immagine direttamente in una delle classi di uscita. Piuttosto, sta imparando una funzione di somiglianza, che prende due immagini come input ed esprime quanto sono simili.

Come si risolvono i due problemi discussi in precedenza?

Tra poco vedremo che per addestrare questa rete non sono necessarie troppe istanze di una classe e ne bastano poche per costruire un buon modello.
Il vantaggio più grande lo si ha nel caso di riconoscimento facciale, quando un nuovo impiegato si unisce all’organizzazione. Per far sì che la rete rilevi il suo volto, abbiamo bisogno di una sola immagine del suo viso, che verrà memorizzata nel database. Utilizzando questa come immagine di riferimento, la rete calcolerà la somiglianza per ogni nuova istanza che le verrà presentata. Si può quindi affermare che la rete predice il punteggio in un colpo solo.

Non preoccupatevi se i dettagli di cui sopra vi sembrano un po’ astratti al momento, continuate e risolveremo un problema in modo dettagliato. Vi prometto che svilupperete una comprensione approfondita dell’argomento.

Applicazioni

Prima di procedere, vorrei menzionare alcune applicazioni dell’apprendimento one shot per motivarvi a sviluppare un interesse più vivo per questa tecnologia.

Come ho già detto a proposito del riconoscimento facciale, basta andare a questo link in cui il guru dell’intelligenza artificiale Andrew Ng dimostra come Baidu (il gigante cinese della ricerca) abbia sviluppato un sistema di riconoscimento facciale per i dipendenti della sua organizzazione.
Leggete questo post per capire come l’apprendimento one shot venga applicato alla scoperta di farmaci, dove i dati sono molto scarsi.
In questo articolo, gli autori hanno utilizzato l’apprendimento one shot per costruire un sistema di verifica offline delle firme, molto utile per le banche e altre istituzioni governative e private.

Dataset omniglot

Per lo scopo di questo post, utilizzeremo il dataset Omniglot: una raccolta di 1623 caratteri disegnati a mano appartenenti a 50 alfabeti diversi. Per ogni carattere ci sono solo 20 esempi, ciascuno disegnato da una persona diversa. Ogni immagine è in scala di grigi con una risoluzione di 105×105.

Prima di continuare, vorrei chiarire la differenza tra un carattere e un alfabeto. Nel caso dell’inglese, l’insieme delle lettere da A a Z è chiamato alfabeto, mentre ciascuna lettera A, B, ecc. è chiamata carattere. Quindi diciamo che l’alfabeto inglese contiene 26 caratteri (o lettere).

Spero che questo chiarisca il concetto di 1623 caratteri che abbracciano oltre 50 alfabeti diversi.

Vediamo alcune immagini di caratteri di diversi alfabeti per avere un’idea più precisa del set di dati.

Abbiamo quindi 1623 classi diverse (ogni carattere può essere trattato come una classe separata) e per ogni classe abbiamo solo 20 immagini. Chiaramente, se cerchiamo di risolvere questo problema utilizzando il metodo tradizionale di classificazione delle immagini, non saremo sicuramente in grado di costruire un buon modello generalizzato. Inoltre, con un numero così basso di immagini disponibili per ogni classe, il modello sarà facilmente overfittato.

È possibile scaricare il set di dati clonando questo repository GitHub. La cartella denominata “Python” contiene due file zip: images_background.zip e images_evaluation.zip. È sufficiente decomprimere questi due file.

La cartella images_background contiene i caratteri di 30 alfabeti e sarà usata per addestrare il modello, mentre la cartella images_evaluation contiene i caratteri degli altri 20 alfabeti che useremo per testare il nostro sistema.

Una volta decompressi i file, si vedranno le seguenti cartelle (alfabeti) nella cartella images_background (usata per l’addestramento):

Contenuti della cartella images_background

E vedrete le cartelle sottostanti (alfabeti) nella cartella images_evaluation (utilizzata per il test)

Contenuti della cartella images_evaluation

Si noti che addestreremo il sistema su un insieme di caratteri e poi lo testeremo su un insieme completamente diverso di caratteri che non sono mai stati utilizzati durante l’addestramento. Questo non è possibile in un ciclo di classificazione tradizionale.

Caricare il dataset

Per prima cosa dobbiamo caricare le immagini in tensori e successivamente usare questi tensori per fornire dati in batch al modello.

Utilizziamo la funzione seguente per caricare le immagini nei tensori:

def loadimgs(path,n = 0):
'''
path => Path of train directory or test directory
'''
X=[]
y = []
cat_dict = {}
lang_dict = {}
curr_y = n

# we load every alphabet seperately so we can isolate them later
for alphabet in os.listdir(path):
print("loading alphabet: " + alphabet)
lang_dict[alphabet] = [curr_y,None]
alphabet_path = os.path.join(path,alphabet)

# every letter/category has it's own column in the array, so load seperately
for letter in os.listdir(alphabet_path):
cat_dict[curr_y] = (alphabet, letter)
category_images=[]
letter_path = os.path.join(alphabet_path, letter)

# read all the images in the current category
for filename in os.listdir(letter_path):
image_path = os.path.join(letter_path, filename)
image = imread(image_path)
category_images.append(image)
y.append(curr_y)
try:
X.append(np.stack(category_images))
# edge case - last one
except ValueError as e:
print(e)
print("error - category_images:", category_images)
curr_y += 1
lang_dict[alphabet][1] = curr_y - 1
y = np.vstack(y)
X = np.stack(X)
return X,y,lang_dict

Per chiamare questa funzione serve passare il percorso della cartella di training come parametro:

X,y,c = loadimgs(train_folder)

La funzione restituisce una tupla di 3 variabili. Non passerò in rassegna ogni riga del codice, ma vi fornirò un’intuizione su cosa fa esattamente la funzione, comprendendo i valori che restituisce. Una volta esaminata questa spiegazione, dovreste essere in grado di capire la funzione di cui sopra.

Cerchiamo di capire cosa c’è in ‘X’:

X.shape
(964, 20, 105, 105)

Ciò significa che abbiamo 964 caratteri (o lettere o categorie) che coprono 30 alfabeti diversi. Per ognuno di questi caratteri, abbiamo 20 immagini e ogni immagine è un’immagine in scala di grigi con risoluzione 105×105. Da qui la forma (964, 20, 105, 105).

Vediamo ora come vengono popolate le etichette ‘y’:

y.shape
(19280, 1)

Numero totale di immagini = 964 * 20 = 19280. Tutte le immagini per una lettera hanno la stessa etichetta, cioè le prime 20 immagini hanno l’etichetta 0, le successive 20 hanno l’etichetta 1, e così via, … le ultime 20 hanno l’etichetta 963.

Infine, l’ultima variabile “c” sta per categorie ed è un dizionario come segue:

c.keys() # 'c' for categoriesdict_keys(['Alphabet_of_the_Magi', 'Anglo-Saxon_Futhorc', 'Arcadian', 'Armenian', 'Asomtavruli_(Georgian)', 'Balinese', 'Bengali', 'Blackfoot_(Canadian_Aboriginal_Syllabics)', 'Braille', 'Burmese_(Myanmar)', 'Cyrillic', 'Early_Aramaic', 'Futurama', 'Grantha', 'Greek', 'Gujarati', 'Hebrew', 'Inuktitut_(Canadian_Aboriginal_Syllabics)', 'Japanese_(hiragana)', 'Japanese_(katakana)', 'Korean', 'Latin', 'Malay_(Jawi_-_Arabic)', 'Mkhedruli_(Georgian)', 'N_Ko', 'Ojibwe_(Canadian_Aboriginal_Syllabics)', 'Sanskrit', 'Syriac_(Estrangelo)', 'Tagalog', 'Tifinagh'])c['Alphabet_of_the_Magi']
[0, 19]c['Anglo-Saxon_Futhorc']
[20, 48]

Poiché esistono 30 alfabeti diversi, questo dizionario ‘c’ contiene 30 voci. La chiave di ogni elemento è il nome dell’alfabeto. Il valore di ogni elemento è un elenco di due numeri: [low, high], dove ‘low’ è l’etichetta del primo carattere di quell’alfabeto e ‘high’ è l’etichetta dell’ultimo carattere di quell’alfabeto.

Una volta caricate le immagini del train e del test, salviamo i tensori sul disco in un file pickle, in modo da poterli utilizzare in seguito direttamente senza dover caricare nuovamente le immagini.

Mappare il problema ad un task di classificazione binaria

Cerchiamo di capire come possiamo mappare questo problema in un compito di apprendimento supervisionato in cui il nostro set di dati contiene coppie di (Xi, Yi) dove ‘Xi’ è l’input e ‘Yi’ è l’output.

Ricordiamo che l’input del nostro sistema sarà una coppia di immagini e l’output sarà un punteggio di similarità tra 0 e 1.

Xi = coppia di immagini

Yi = 1, se entrambe contengono la stessa persona

Yi = 0, se le immagini contengono persone diverse

Cerchiamo di capire meglio la situazione visualizzando il dataset qua sotto:

Pertanto, dobbiamo creare coppie di immagini insieme alla variabile target, come mostrato sopra, da dare in ingresso alla rete siamese. Si noti che anche se i caratteri dell’alfabeto sanscrito sono mostrati qui sopra, in pratica genereremo le coppie in modo casuale da tutti gli alfabeti presenti nei dati di addestramento.

Il codice per generare queste coppie e gli obiettivi è mostrato di seguito:

def get_batch(batch_size,s="train"):
"""
Create batch of n pairs, half same class, half different class
"""
if s == 'train':
X = Xtrain
categories = train_classes
else:
X = Xval
categories = val_classes
n_classes, n_examples, w, h = X.shape

# randomly sample several classes to use in the batch
categories = rng.choice(n_classes,size=(batch_size,),replace=False)

# initialize 2 empty arrays for the input image batch
pairs=[np.zeros((batch_size, h, w,1)) for i in range(2)]

# initialize vector for the targets
targets=np.zeros((batch_size,))

# make one half of it '1's, so 2nd half of batch has same class
targets[batch_size//2:] = 1
for i in range(batch_size):
category = categories[i]
idx_1 = rng.randint(0, n_examples)
pairs[0][i,:,:,:] = X[category, idx_1].reshape(w, h, 1)
idx_2 = rng.randint(0, n_examples)

# pick images of same class for 1st half, different for 2nd
if i >= batch_size // 2:
category_2 = category 
else:
# add a random number to the category modulo n classes to ensure 2nd image has a different category
category_2 = (category + rng.randint(1,n_classes)) % n_classes

pairs[1][i,:,:,:] = X[category_2,idx_2].reshape(w, h,1)

return pairs, targets

È necessario richiamare la funzione di cui sopra passandole il batch_size e questa restituirà il numero “batch_size” di coppie di immagini insieme alle loro variabili di destinazione.

Utilizzeremo la funzione generatrice qui sotto per generare dati in lotti (batches) durante l’addestramento della rete.

def generate(batch_size, s="train"):
"""
a generator for batches, so model.fit_generator can be used.
"""
while True:
pairs, targets = get_batch(batch_size,s)
yield (pairs, targets)

Architettura del modello e addestramento

Questo codice è un’implementazione della metodologia descritta in questo articolo di Gregory Koch et al. L’architettura del modello e gli iperparametri che ho utilizzato sono tutti descritti nell’articolo.

Prima di immergerci nei dettagli, cerchiamo di capire l’architettura ad alto livello. Di seguito presento un’intuizione dell’architettura.

Intuizione: Il termine siamese significa gemelli. Le due reti neurali convoluzionali mostrate sopra non sono reti diverse, ma due copie della stessa rete, da cui il nome di reti siamesi. In pratica, condividono gli stessi parametri. Le due immagini di ingresso (x1 e x2) vengono fatte passare attraverso la rete neurale convoluzionale per generare un vettore di caratteristiche di lunghezza fissa per ciascuna di esse (h(x1) e h(x2)). Supponendo che il modello di rete neurale sia stato addestrato correttamente, possiamo formulare la seguente ipotesi: Se le due immagini in ingresso appartengono alla stessa persona, anche i loro vettori di caratteristiche devono essere simili, mentre se le due immagini in ingresso appartengono a persone diverse, anche i loro vettori di caratteristiche saranno diversi. Pertanto, la differenza assoluta tra i due vettori di caratteristiche deve essere molto diversa in entrambi i casi. Di conseguenza, anche il punteggio di somiglianza generato dallo strato sigmoide di uscita deve essere diverso in questi due casi. Questa è l’idea centrale delle reti siamesi.

Data l’intuizione di cui sopra, diamo un’occhiata all’immagine dell’architettura con maggiori dettagli tratti dal documento di ricerca stesso:

La funzione sottostante viene utilizzata per creare l’architettura del modello:

def get_siamese_model(input_shape):
"""
Model architecture
"""

# Define the tensors for the two input images
left_input = Input(input_shape)
right_input = Input(input_shape)

# Convolutional Neural Network
model = Sequential()
model.add(Conv2D(64, (10,10), activation='relu', input_shape=input_shape,
kernel_initializer=initialize_weights, kernel_regularizer=l2(2e-4)))
model.add(MaxPooling2D())
model.add(Conv2D(128, (7,7), activation='relu',
kernel_initializer=initialize_weights,
bias_initializer=initialize_bias, kernel_regularizer=l2(2e-4)))
model.add(MaxPooling2D())
model.add(Conv2D(128, (4,4), activation='relu', kernel_initializer=initialize_weights,
bias_initializer=initialize_bias, kernel_regularizer=l2(2e-4)))
model.add(MaxPooling2D())
model.add(Conv2D(256, (4,4), activation='relu', kernel_initializer=initialize_weights,
bias_initializer=initialize_bias, kernel_regularizer=l2(2e-4)))
model.add(Flatten())
model.add(Dense(4096, activation='sigmoid',
kernel_regularizer=l2(1e-3),
kernel_initializer=initialize_weights,bias_initializer=initialize_bias))

# Generate the encodings (feature vectors) for the two images
encoded_l = model(left_input)
encoded_r = model(right_input)

# Add a customized layer to compute the absolute difference between the encodings
L1_layer = Lambda(lambda tensors:K.abs(tensors[0] - tensors[1]))
L1_distance = L1_layer([encoded_l, encoded_r])

# Add a dense layer with a sigmoid unit to generate the similarity score
prediction = Dense(1,activation='sigmoid',bias_initializer=initialize_bias)(L1_distance)

# Connect the inputs with the outputs
siamese_net = Model(inputs=[left_input,right_input],outputs=prediction)

# return the model
return siamese_net

Si noti che non esiste un livello predefinito in Keras per calcolare la differenza assoluta tra due tensori. Lo facciamo usando il livello Lambda di Keras, che serve per aggiungere livelli personalizzati in Keras.

Per capire la forma dei tensori passati ai diversi livelli, si veda l’immagine seguente generata con l’utilità plot_model di Keras.

Il modello è stato compilato utilizzando l’ottimizzatore Adam e la funzione di perdita binary cross entropy, come mostrato di seguito. Il learning rate è stato mantenuto basso poiché si è riscontrato che con un tasso di apprendimento elevato il modello richiedeva molto tempo per convergere. Tuttavia, questi parametri possono essere ulteriormente regolati per migliorare le impostazioni attuali.

optimizer = Adam(lr = 0.00006)
model.compile(loss="binary_crossentropy",optimizer=optimizer)

Il modello è stato addestrato per 20000 iterazioni con una dimensione di batch di 32.

Dopo ogni 200 iterazioni, viene fatta la validazione del modello utilizzando l’apprendimento one shot con 20 vie e l’accuratezzza è stata calcolata su 250 prove. Questo concetto è spiegato nella prossima sezione.

Validare il modello

Ora che abbiamo capito come preparare i dati per l’addestramento, l’architettura del modello e l’addestramento, è il momento di pensare a una strategia per validare e testare il nostro modello.

Si noti che, per ogni coppia di immagini in ingresso, il nostro modello genera un punteggio di somiglianza compreso tra 0 e 1. Ma solo guardando il punteggio è difficile accertare se il modello è davvero in grado di riconoscere caratteri simili e distinguere quelli dissimili.

Un modo efficace per giudicare il modello è l’apprendimento N-way one shot. Non preoccupatevi, è molto più semplice di quanto sembri.

Un esempio di apprendimento one shot a 4 vie (4-way):

In pratica, lo stesso carattere viene confrontato con 4 caratteri diversi, di cui solo uno corrisponde al carattere originale. Supponiamo che facendo i 4 confronti di cui sopra otteniamo 4 punteggi di somiglianza S1, S2, S3 e S4 come mostrato. Se il modello è stato addestrato correttamente, ci aspettiamo che S1 sia il massimo di tutti e 4 i punteggi di somiglianza, perché la prima coppia di immagini è l’unica in cui ci sono due personaggi uguali.

Quindi, se S1 è il punteggio massimo, lo consideriamo come una previsione corretta, altrimenti lo consideriamo come una previsione errata. Ripetendo questa procedura ‘k’ volte, possiamo calcolare la percentuale di previsioni corrette come segue:

percentuale_corretta = (100 * n_corretta) / k

dove k => numero totale di prove e n_corretto => numero di previsioni corrette su k prove.

Allo stesso modo, un apprendimento a 9 vie one shot avrà il seguente aspetto:

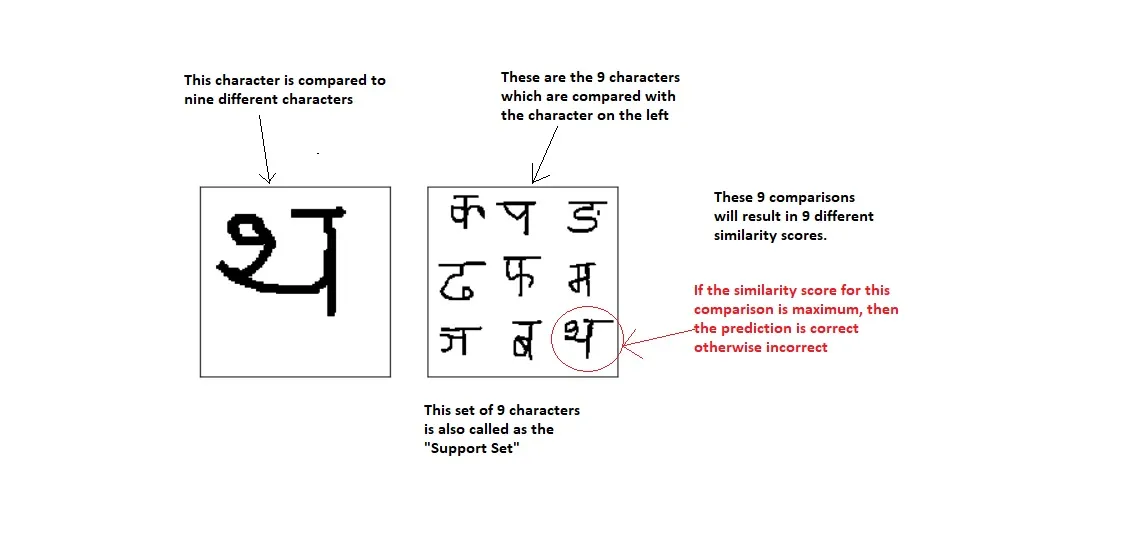
Un apprendimento a 16 vie sarà come mostrato di seguito:

Mentre uno a 25 vie:

Si noti che il valore di ‘N’ nell’apprendimento a una via non deve necessariamente essere un quadrato perfetto. Il motivo per cui ho scelto i valori 4, 9, 16 e 25 è che il quadrato è riempito completamente, per una buona presentazione.

È abbastanza ovvio che valori più piccoli di ‘N’ porteranno a un maggior numero di previsioni corrette e valori più grandi di ‘N’ porteranno a previsioni relativamente meno corrette se ripetute più volte.

Ricordiamo ancora una volta: Tutti gli esempi mostrati sopra provengono dall’alfabeto sanscrito, ma in pratica genereremo l’immagine di prova e l’insieme di supporto in modo casuale da tutti gli alfabeti delle immagini del dataset di prova/validazione.

Il codice per generare l’immagine di prova e l’insieme di supporto è il seguente:

def make_oneshot_task(N, s="val", language=None):
"""Create pairs of test image, support set for testing N way one-shot learning. """
if s == 'train':
X = Xtrain
categories = train_classes
else:
X = Xval
categories = val_classes
n_classes, n_examples, w, h = X.shape

indices = rng.randint(0, n_examples,size=(N,))
if language is not None: # if language is specified, select characters for that language
low, high = categories[language]
if N > high - low:
raise ValueError("This language ({}) has less than {} letters".format(language, N))
categories = rng.choice(range(low,high),size=(N,),replace=False)
else: # if no language specified just pick a bunch of random letters
categories = rng.choice(range(n_classes),size=(N,),replace=False) 

true_category = categories[0]
ex1, ex2 = rng.choice(n_examples,replace=False,size=(2,))
test_image = np.asarray([X[true_category,ex1,:,:]]*N).reshape(N, w, h,1)
support_set = X[categories,indices,:,:]
support_set[0,:,:] = X[true_category,ex2]
support_set = support_set.reshape(N, w, h,1)
targets = np.zeros((N,))
targets[0] = 1
targets, test_image, support_set = shuffle(targets, test_image, support_set)
pairs = [test_image,support_set]
return pairs, targets


def test_oneshot(model, N, k, s = "val", verbose = 0):
"""Test average N way oneshot learning accuracy of a siamese neural net over k one-shot tasks"""
n_correct = 0
if verbose:
print("Evaluating model on {} random {} way one-shot learning tasks ... \n".format(k,N))
for i in range(k):
inputs, targets = make_oneshot_task(N,s)
probs = model.predict(inputs)
if np.argmax(probs) == np.argmax(targets):
n_correct+=1
percent_correct = (100.0 * n_correct / k)
if verbose:
print("Got an average of {}% {} way one-shot learning accuracy \n".format(percent_correct,N))
return percent_correct

Baseline

Baseline 1 – Modello Nearest Neighbour

È sempre una buona pratica creare modelli di base semplici e confrontare i loro risultati con il modello complesso che si sta cercando di costruire.

Il nostro primo modello di riferimento è l’approccio Nearest Neighbor. Se conoscete l’algoritmo K-Nearest Neighbor, si tratta della stessa cosa.

Come discusso in precedenza, in un apprendimento one shot a N vie, confrontiamo un’immagine di prova con N immagini diverse e selezioniamo l’immagine che ha la massima somiglianza con l’immagine di prova come predizione.

Si tratta di un metodo intuitivamente simile al KNN con K=1. Vediamo nel dettaglio come funziona questo approccio.

Forse avete studiato come si calcola la distanza L2 (detta anche distanza euclidea) tra due vettori. Se non lo ricordate, ecco come si fa:

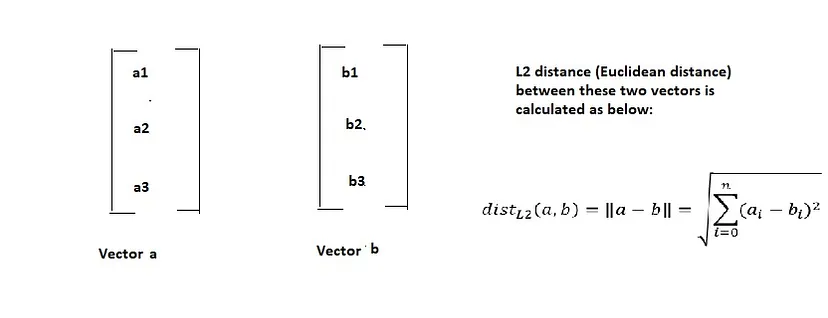
Supponiamo di confrontare la distanza L2 di un vettore X con altri 3 vettori, ad esempio A, B e C. Allora un modo per calcolare il vettore più simile a X è verificare quale vettore ha la minore distanza L2 con X. Perché la distanza è inversamente proporzionale alla somiglianza. Quindi, ad esempio, se la distanza L2 tra X e B è minima, diciamo che la somiglianza tra X e B è massima.

Tuttavia, nel nostro caso non abbiamo vettori ma immagini in scala di grigi, che possono essere rappresentate come matrici e non come vettori. Come si calcola allora la distanza L2 tra matrici?

È semplice, basta appiattire le matrici in vettori e poi calcolare la distanza L2 tra questi vettori. Per esempio:

Nell’apprendimento N-way One Shot, quindi, si confronta la distanza L2 dell’immagine di prova con tutte le immagini dell’insieme di supporto. Nel caso dei caratteri, si controlla quello per il quale si è ottenuta la distanza L2 minima. Se questo carattere è uguale a quello dell’immagine di prova, la previsione è corretta, altrimenti è errata. Ad esempio:

Come nel caso dell’apprendimento one shot a N vie, si ripete l’operazione per più prove e si calcola il punteggio medio di predizione su tutte le prove. Il codice per l’approccio nearest neighbor è riportato di seguito:

def nearest_neighbour_correct(pairs,targets):

"""returns 1 if nearest neighbour gets the correct answer for a one-shot task

     given by (pairs, targets)"""

L2_distances = np.zeros_like(targets)

for i in range(len(targets)):

     L2_distances[i] = np.sum(np.sqrt(pairs[0][i]**2 - pairs[1][i]**2))

if np.argmin(L2_distances) == np.argmax(targets):

     return 1

return 0




  def test_nn_accuracy(N_ways,n_trials):

"""Returns accuracy of NN approach """

print("Evaluating nearest neighbour on {} unique {} way one-shot learning tasks ...".format(n_trials,N_ways))

n_right = 0

    

for i in range(n_trials):

     pairs,targets = make_oneshot_task(N_ways,"val")

     correct = nearest_neighbour_correct(pairs,targets)

     n_right += correct

return 100.0 * n_right / n_trials

Baseline 2 – Modello Random

Creare un modello casuale che faccia previsioni a caso è una tecnica molto comune per assicurarsi che il modello creato sia almeno migliore di un modello che fa previsioni completamente casuali. Il suo funzionamento può essere riassunto nel diagramma seguente:

Risultati e conclusione

I test a N sono stati eseguiti per N = 1, 3, 5, …., 19.

Per ogni test sono state eseguite 50 prove e l’accuratezza media è stata calcolata su queste 50 prove.

Di seguito è riportato il confronto tra i 4 modelli:

Inferenza: È evidente che il modello siamese ha ottenuto risultati migliori rispetto al modello casuale e al modello Nearest Neighbour. Tuttavia, c’è un certo divario tra i risultati del training set e quelli del validation set, che indica che il modello si overfitta.

Conclusione

Questa è solo una prima soluzione e molti degli iperparametri possono essere regolati per evitare l’overfitting. Inoltre, è possibile eseguire test più rigorosi aumentando il valore di ‘N’ nei test a N vie e aumentando il numero di prove.

Spero che questo vi abbia aiutato a capire la metodologia di apprendimento one shot con il Deep Learning.

Codice: Consultate con Jupyter Notebook il mio codice che si trova sul mio repository GitHub.

Note: Il modello è stato addestrato on Cloud con una GPU P4000. Se lo addestrate su una CPU, dovete portare molta pazienza.

Commenti, suggerimenti e critiche sono i benvenuti. Grazie!

References