Outliers nel Machine Learning: comprendere il loro impatto sull’analisi dei dati
Articolo in lingua originale di Vishal Sharma
Il Machine Learning è uno strumento potente che può aiutare le aziende a estrarre
preziose intuizioni da grandi quantità di dati. Tuttavia, non è privo di sfide. Una delle sfide più significative che i professionisti del machine learning affrontano
è la presenza di outlier nei loro set di dati.

Gli outlier sono dati che si trovano molto al di fuori dell’intervallo rispetto alla maggior parte degli altri dati in un determinato set. Possono essere dovuti a errori di misurazione, errori di inserimento dei dati o a un’anomalia nei dati. Gli outlier possono influenzare in modo significativo i risultati dei modelli di machine learning, causando previsioni imprecise e analisi distorte dei dati.
In questo articolo discuteremo l’impatto degli outlier sul machine learning ed esploreremo alcune tecniche standard per gestirli.
L’impatto degli outliers nel machine learning
Gli outlier possono avere un impatto significativo sulle prestazioni dei modelli di machine learning. Possono influire sull’accuratezza dei modelli e portare a previsioni errate. Ad esempio, in un modello di regressione, i valori anomali possono determinare una deviazione significativa dalla linea di miglior fit dei dati, con conseguenti previsioni imprecise.
Gli outlier possono anche influenzare l’addestramento dei modelli di machine learning. Quando nel training set sono presenti degli outlier, il modello può diventare eccessivamente sensibile a questi punti, causando un overfitting. L’overfitting si verifica quando il modello diventa troppo complesso e si adatta troppo strettamente ai dati di training, con conseguenti scarse prestazioni su dati nuovi e non visti.
import numpy as np
import matplotlib.pyplot as plt
# Generate random data
np.random.seed(42)
x = np.random.normal(0, 1, 100)
y = 2 * x + 1 + np.random.normal(0, 0.5, 100)
# Add some outliers
x_outliers = np.random.normal(5, 1, 5)
y_outliers = np.random.normal(5, 1, 5)
x = np.concatenate((x, x_outliers))
y = np.concatenate((y, y_outliers))
fig, ax = plt.subplots(figsize=(10, 6))
main_color = 'green'
outlier_color = 'red'
alpha_main = 0.6
alpha_outliers = 0.8
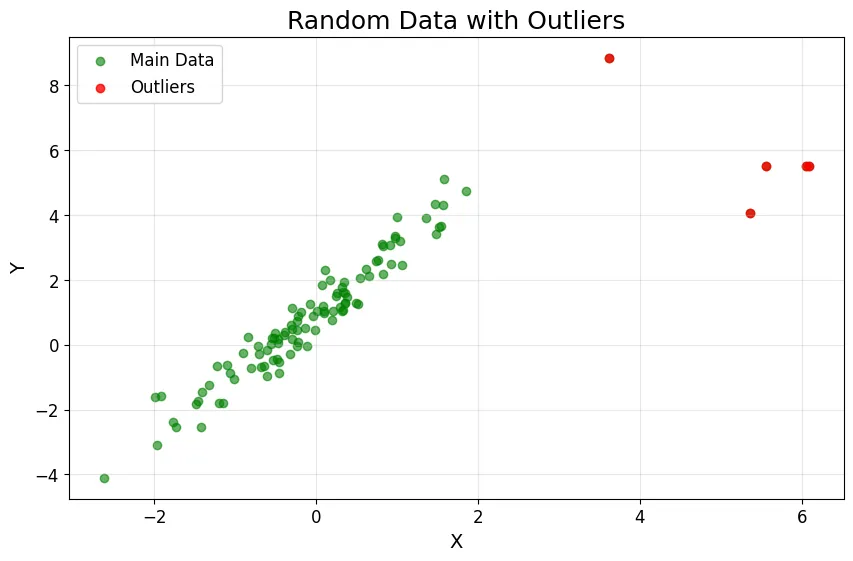
ax.scatter(x, y, c=main_color, alpha=alpha_main, label='Main Data')
ax.scatter(x_outliers, y_outliers, c=outlier_color, alpha=alpha_outliers, label='Outliers')
ax.legend(loc='upper left', fontsize=12)
ax.set_title('Random Data with Outliers', fontsize=18)
ax.set_xlabel('X', fontsize=14)
ax.set_ylabel('Y', fontsize=14)
ax.grid(alpha=0.3)
ax.tick_params(axis='both', which='major', labelsize=12)
plt.show()
import numpy as np
import pandas as pd
import seaborn as sns
import matplotlib.pyplot as plt
# Define the original and outlier data
data = [15, 101, 18, 7, 13, 16, 11, 21, 5, 15, 10, 9]
data_without_outlier = [d for d in data if d < 50]
# Create a summary dataframe for original and outlier data
summary = pd.DataFrame({
'Original Data': np.round(pd.Series(data).describe(), 2),
'Data without Outlier': np.round(pd.Series(data_without_outlier).describe(), 2)
})
sns.set_palette('pastel')
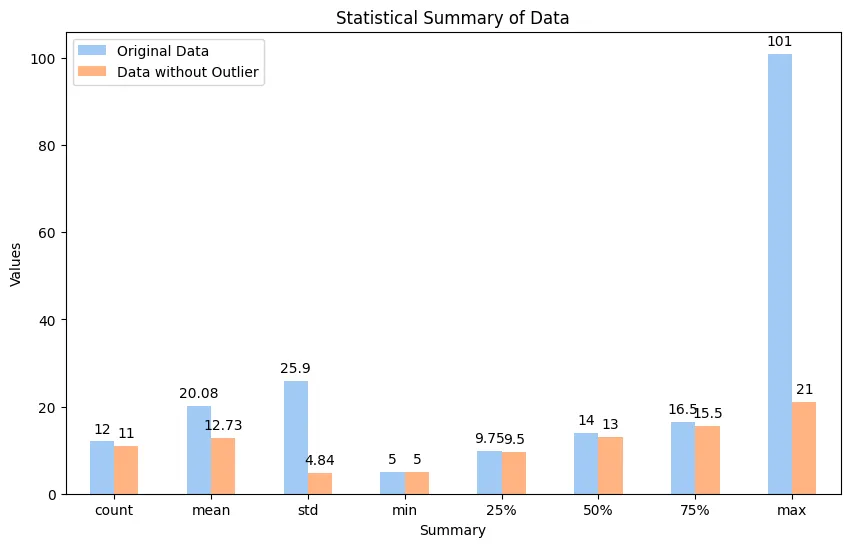
ax = summary.plot(kind='bar', rot=0, figsize=(10,8))
ax.set_title('Statistical Summary of Data')
ax.set_xlabel('Summary')
ax.set_ylabel('Values')
# Add the values to the bars
for i in ax.containers:
ax.bar_label(i, label_type='edge', fontsize=10, padding=4)
# Show the plot
plt.show()
Tecniche comuni per gestire gli outliers
Ci sono diverse tecniche standard per gestire gli outliers nel machine learning. Ne affronteremo 3 di queste.
Metodo Z-Score
Il metodo Z-score è un metodo semplice ed efficace per identificare e rimuovere gli outlier.
Il metodo del punteggio Z è un metodo semplice ed efficace per identificare e rimuovere gli outlier. Lo Z-score viene calcolato sottraendo la media da ciascun dato e dividendo il risultato per la deviazione standard. Qualsiasi punto di dati con uno Z-score più significativo di una soglia specificata (di solito 3 o -3) è considerato un outlier e può essere rimosso dal set di dati.
# Generate random data with some outliers data = np.concatenate([np.random.normal(0, 1, 50), [10, -10]]) # Calculate Z-scores for each data point z_scores = (data - np.mean(data)) / np.std(data) # Define threshold for outlier detection z_thresh = 3 # Identify and remove outliers outliers = np.where(np.abs(z_scores) > z_thresh)[0] clean_data = np.delete(data, outliers) # Plot the original data and the cleaned data fig, ax = plt.subplots(figsize=(10, 6)) ax.scatter(range(len(data)), data, label="Original Data") ax.scatter(range(len(clean_data)), clean_data, label="Cleaned Data") ax.axhline(np.mean(data), linestyle="--", color="black", label="Mean") ax.axhline(np.mean(data) + z_thresh * np.std(data), linestyle="--", color="red", label="Threshold") ax.axhline(np.mean(data) - z_thresh * np.std(data), linestyle="--", color="red") ax.legend() plt.show()
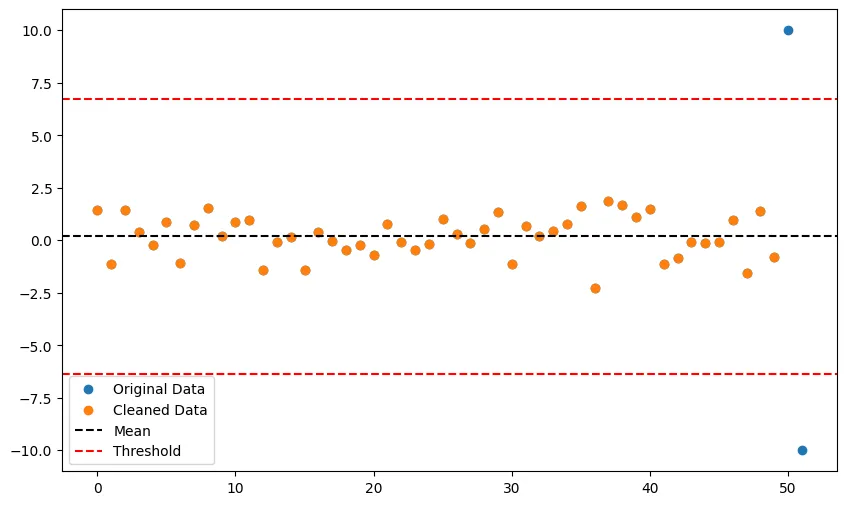
Questo codice genera un set di dati casuali con 50 campioni normalmente distribuiti e aggiunge due outlier (uno positivo e uno negativo). Calcola quindi gli Z-score per ogni dato e imposta una soglia di 3 per il rilevamento degli outlier. Qualsiasi campione con un punteggio Z superiore a 3 o inferiore a -3 è considerato un outlier e viene rimosso dal set di dati. I dati puliti vengono quindi mostrati insieme ai dati originali, con le linee della media e della soglia come riferimento.
Metodo Range Interquartile (IQR)
Il metodo del range interquartile è un altro metodo per identificare gli outliers. L’IQR è il range tra il primo quartile dei dati (25esimo percentile) e il terzo quartile (75esimo percentile). Qualsiasi dato al di fuori del range IQR di 1.5 volte viene considerato outlier e può essere rimosso dal dataset.
# Generate random data with some outliers data = np.concatenate([np.random.normal(0, 1, 50), [10, -10]]) # Calculate quartiles and IQR q1, q3 = np.percentile(data, [25, 75]) iqr = q3 - q1 # Define threshold for outlier detection iqr_thresh = 1.5 # Identify and remove outliers lower_thresh = q1 - iqr_thresh * iqr upper_thresh = q3 + iqr_thresh * iqr outliers = np.where((data < lower_thresh) | (data > upper_thresh))[0] clean_data = np.delete(data, outliers) fig, ax = plt.subplots(figsize=(10, 6)) ax.scatter(range(len(data)), data, label="Original Data") ax.scatter(range(len(clean_data)), clean_data, label="Cleaned Data") ax.axhline(q1, linestyle="--", color="black", label="Q1") ax.axhline(q3, linestyle="--", color="black", label="Q3") ax.axhline(lower_thresh, linestyle="--", color="red", label="Threshold") ax.axhline(upper_thresh, linestyle="--", color="red") ax.legend() plt.show()
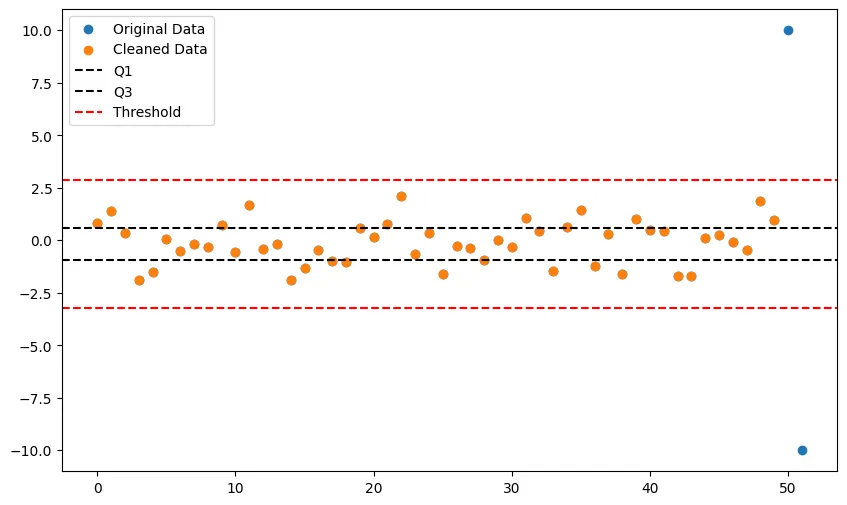
Questo codice genera un seit di dati casuali con 50 campioni distribuiti normalmente e aggiunge 2 outliers (uno positivo e uno negativo). Calcoal poi i quartili e l’IQR del dataset. Una soglia di 1.5 volte il range IQR viene impostata per identificare gli outliers. Qualsiasi dati al di fuori di questo range viene considerato un outlier e rimosso dal dataset. I dati puliti sono poi plottati insieme a quelli originali con la linea dei quartili e della soglia come riferimento.
Regressione robusta
La regressione robusta è un metodo meno sensibile agli outlier rispetto alla regressione tradizionale. La regressione robusta utilizza una funzione di costo diversa da quella della regressione tradizionale, che attribuisce un peso minore agli outlier. Questo metodo è in grado di gestire efficacemente gli insiemi di dati contenenti pochi outlier.
import matplotlib.pyplot as plt
import numpy as np
from sklearn.linear_model import RANSACRegressor
# Initialize RANSAC Regressor
ransac = RANSACRegressor()
# Fit the model
ransac.fit(X, y)
# Obtain the inlier mask
inlier_mask = ransac.inlier_mask_
# Obtain the outlier data
outlier_X = X[~inlier_mask]
outlier_y = y[~inlier_mask]
# Generate data for the regression line
line_X = np.arange(X.min(), X.max())[:, np.newaxis]
line_y = ransac.predict(line_X)
fig, ax = plt.subplots(figsize=(10, 6))
ax.scatter(X[inlier_mask], y[inlier_mask], c='green', marker='o', label='Inliers')
ax.scatter(outlier_X, outlier_y, c='red', marker='x', label='Outliers')
ax.plot(line_X, line_y, color='black', linewidth=2, label='Robust Regression')
ax.legend(fontsize=12)
ax.set_xlabel('X', fontsize=14)
ax.set_ylabel('Y', fontsize=14)
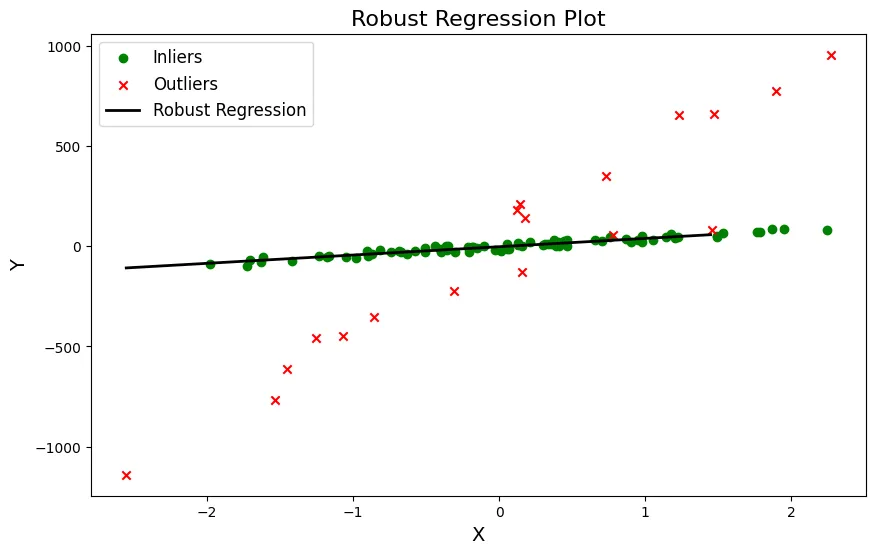
ax.set_title('Robust Regression Plot', fontsize=16)
plt.show()
Questo codice genera un set di dati casuali con 100 campioni e aggiunge 20 outliers ai loro valori y. Fitta poi un modello di regressione robusta utilizzando l’algoritmo RANSAC che è meno sensibile agli outliers rispetto alla regressione lineare tradizionale. Gli outlier vengono predetti separatamente dagli inlier, i dati originali e la linea di regressione robusta sono plottati insieme.
Conclusione
Gli outlier possono impattare significativamente sulle performance dei modelli di machine learning. Identificare e gestire gli outlier è cruciale per assicurare predizioni accurate ed un’analisi dati affidabile. Ci sono diverse tecniche per gestire gli outlier, incluso il metodo Z-score, il metodo del range interquartile e la regressione robusta. Comprendere e applicare queste tecniche può portare a risultati migliori ed un’analisi dati più efficace.
Share: