Previsione multivariata delle serie temporali con i trasformatori

Temporal Self-Attention (left) and Spatiotemporal Self-Attention (right). Splitting each timestep into separate time series variab.

Molte applicazioni reali del Machine Learning prevedono la formulazione di previsioni sui risultati di un gruppo di variabili correlate, basate su un contesto storico. Potremmo voler prevedere le condizioni del traffico su strade collegate, il tempo nelle località vicine o la domanda di prodotti simili. Modellando più serie temporali insieme, speriamo che le variazioni di una variabile possano rivelare informazioni chiave sul comportamento delle variabili correlate. Le serie temporali multivariate di dati (TSF) presentano due assi di difficoltà: dobbiamo imparare le relazioni temporali per capire come i valori cambiano nel tempo e le relazioni spaziali per sapere come le variabili si influenzano a vicenda.

Per approfondire meglio questi argomenti, nel caso non vi sentiste abbastanza preparati, vi consigliamo il nostro corso di Deep Learning per il Sequence Modelling e le Time Series che include anche una lezione sulle serie multivariate!

Gli approcci statistici più diffusi al TSF possono faticare a interpretare lunghe sequenze di contesti e ad adattarsi a relazioni complesse tra le variabili. I modelli di apprendimento profondo superano queste sfide utilizzando grandi insiemi di dati per prevedere eventi rari in un futuro lontano. Molti metodi si concentrano sull’apprendimento di modelli temporali su lunghi archi temporali e si basano su strati ricorrenti o convoluzionali. In domini altamente spaziali, le reti neurali grafiche (GNN) possono analizzare le relazioni tra le variabili come un grafo di nodi connessi. Questo grafo è spesso predefinito, ad esempio una mappa di strade e incroci nella previsione del traffico.

In questo post intendiamo spiegare il nostro recente lavoro su un modello ibrido che apprende un grafo sia nello spazio che nel tempo, partendo esclusivamente dai dati. Convertiamo il TSF multivariato in un problema di predizione di sequenze molto lunghe, risolvibile grazie ai recenti miglioramenti apportati all’architettura di Transformer. L’approccio porta a risultati competitivi in domini che vanno dalla previsione della temperatura a quella del traffico e dell’energia.

Questo è un riassunto informale del nostro lavoro di ricerca, “Long-Range Transformers for Dynamic Spatiotemporal Forecasting”, Grigsby, Wang e Qi, 2021. Il documento è disponibile su arXiv e tutto il codice necessario per replicare gli esperimenti e applicare il modello a nuovi problemi è disponibile su GitHub.

I trasformatori e la previsione delle serie temporali

I trasformatori sono una soluzione all’avanguardia per le attività di elaborazione del linguaggio naturale (NLP). Si basano sul meccanismo Multihead-Self-Attention (MSA), in cui ogni token della sequenza di input viene confrontato con ogni altro token per raccogliere informazioni e apprendere informazioni contestuali dinamiche. Il trasformatore apprende un grafo di passaggio di informazioni tra i suoi ingressi. Poiché non analizzano i loro input in modo sequenziale, i Transformer risolvono in gran parte il problema del gradiente che ostacola le reti neurali ricorrenti (RNN) nella predizione a lungo termine. Per questo motivo, i trasformatori sono stati applicati a insiemi di dati con lunghe informazioni storiche, tra cui i TSF.

I dataset TSF multivariati sono solitamente organizzati per tempo: i valori di tutte le N variabili sono rappresentati come un unico vettore. Tuttavia, ciò consente ai trasformatori di apprendere solo le relazioni tra l’intera pila di variabili nel tempo. Nei problemi complessi di TSF multivariato, ogni variabile ha relazioni significative con la sua storia e con i diversi eventi nella storia di altre variabili. Un’applicazione standard di Transformers ai dati TSF non è in grado di apprendere questo aspetto, perché tratta i valori di ogni variabile in un dato momento come un singolo token nel suo grafo; ogni variabile non può avere una propria opinione sul contesto a cui dovrebbe dare priorità. Questo a differenza dei compiti di NLP in cui i Transformers sono così popolari, dove ogni token rappresenta un’idea unificata (una singola parola).

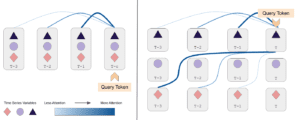
Per risolvere questo problema, abbiamo creato un nuovo problema di predizione in cui ogni token rappresenta il valore di una singola variabile per ogni passo temporale. I trasformatori sono quindi liberi di occuparsi dei valori di qualsiasi variabile in qualsiasi momento, per fare previsioni più accurate. Il diagramma in cima a questo post mostra la differenza tra questi due tipi di attenzione.

Spacetimeformer

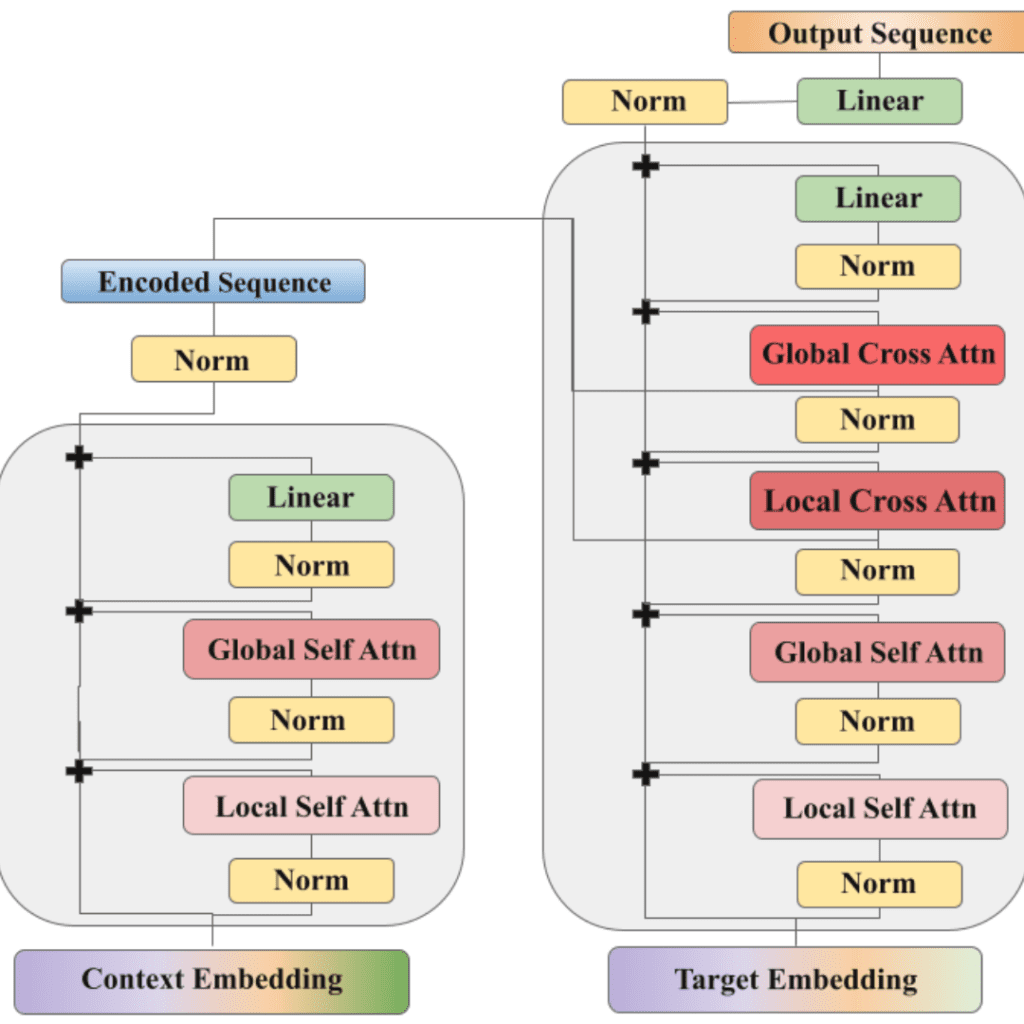
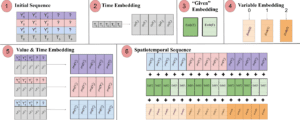
Utilizziamo un formato di input in cui N variabili a T timestep sono appiattite in una sequenza di (N x T) token. Il valore di ogni variabile viene proiettato in uno spazio ad alta dimensione con uno strato feed-forward. Si aggiungono poi informazioni sul tempo e sulla variabile corrispondenti a ciascun token. Le incorporazioni di tempo e variabile sono inizializzate in modo casuale e addestrate con il resto del modello per migliorare la rappresentazione delle relazioni temporali e spaziali. I valori a intervalli di tempo futuri che vogliamo prevedere sono impostati a zero e indichiamo al modello quali sono quelli mancanti con un embedding binario “dato”. I diversi componenti vengono sommati e disposti in modo tale che Transformer MSA costruisca un grafo spaziotemporale nel tempo e nello spazio variabile. La pipeline di embedding è visualizzata nella figura seguente.

Spatiotemporal Sequence Inputs: (1) The multivariate input format with time information included. Decoder inputs have missing (“?”) values set to zero where predictions will be made. (2) The time sequence is passed through a Time2Vec layer to generate a frequency embedding that represents periodic input patterns. (3) A binary embedding indicates whether this value is given as context or needs to be predicted. (4) The integer index of each time series is mapped to a “spatial” representation with a lookup-table embedding. (5) The Time2Vec embedding and variable values of each time series are projected with a feed-forward layer. (6) Value&Time, Variable, and Given embeddings are summed and laid out such that MSA attends to relationships across both time and variable space at the cost of a longer input sequence.

I trasformatori standard confrontano ogni token con ogni altro token per trovare informazioni rilevanti nella sequenza. Ciò significa che il tempo di esecuzione e l’uso della memoria del modello crescono quadraticamente con la lunghezza totale del suo input. Il nostro metodo esagera notevolmente questo problema, rendendo la sequenza N volte più lunga della serie temporale stessa. Il resto del nostro approccio affronta la sfida ingegneristica di rendere possibile l’addestramento di questo modello senza le GPU/TPU più potenti.

I trasformatori efficienti sono un’area di ricerca attiva nelle applicazioni con sequenze di ingresso lunghe. Questi “trasformatori a lungo raggio” cercano di adattare il calcolo del gradiente delle sequenze più lunghe alla memoria della GPU. Spesso lo fanno aggiungendo un’euristica per rendere il grafo dell’attenzione più rado, ma questi presupposti non sono sempre validi al di fuori dell’NLP. Noi usiamo il meccanismo di attenzione Performer, che approssima linearmente l’MSA con un kernel di caratteristiche casuali. Performer è abbastanza efficiente da adattarsi a sequenze di migliaia di token e ci permette di addestrare il nostro modello in poche ore su un nodo con GPU da 10 GB.

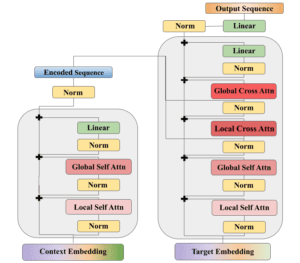
La sequenza contestuale di dati storici e i timestamp di destinazione che vogliamo prevedere vengono convertiti in lunghe sequenze spazio-temporali. Un’architettura di codifica-decodifica basata su Performer elabora la sequenza e predice il valore di ciascuna variabile a intervalli di tempo futuri come token separati. Possiamo quindi impilare nuovamente le previsioni nel loro formato originale e allenarci a minimizzare le metriche di errore di previsione, come l’errore quadratico medio. Il modello può anche creare una gamma di previsioni, fornendo sia la media che la deviazione standard di una distribuzione normale, nel qual caso ci alleniamo per massimizzare la probabilità della sequenza di verità. L’architettura completa del modello è illustrata di seguito.

Spacetimeformer Architecture: Target and Context Embeddings are passed through a sequence of effiicient attention layers. “Global Attention” modules looks at every timestep of every variable while “Local Attention” sees the timesteps of each variable separately. We found this to be helpful in datasets with large N.

Applicazioni

Confrontiamo il modello con i metodi TSF e GNN più standard. Linear AR è un modello lineare di base addestrato per fare previsioni auto-regressive, cioè emette un token alla volta e ricicla il suo risultato come input per la previsione successiva. LSTM è un modello standard di codificatore-decodificatore basato su RNN senza attenzione. LSTNet è un modello autoregressivo basato su strati Conv1D e RNN con connessioni di salto per ricordare il contesto a lungo termine. DCRNN è un modello basato su un grafo che può essere utilizzato quando è disponibile un grafo di variabili predefinito. Come il nostro metodo, MTGNN è un ibrido TSF/GNN che apprende la sua struttura a grafo dai dati, ma non utilizza i trasformatori per la previsione temporale. Infine, includiamo una versione del nostro modello che non separa i token in un grafo spazio-temporale; i valori di ogni variabile rimangono impilati insieme come al solito. Questa ablazione “temporale” è una controfigura di Informer, ma utilizza tutti gli altri trucchi ingegneristici e il processo di addestramento per isolare i vantaggi dell’attenzione spaziotemporale.
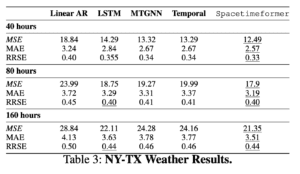
Per prima cosa, analizzeremo un compito di previsione del tempo. Abbiamo utilizzato la rete ASOS per mettere insieme un ampio set di dati di letture della temperatura provenienti da aeroporti del Texas e di New York. La separazione geografica tra i due gruppi rende più importanti le relazioni spaziali, che devono essere apprese dall’esperienza perché non forniamo alcuna informazione sulla posizione. Prevediamo 40, 80 e 160 ore nel futuro e confrontiamo l’errore quadratico medio (MSE), l’errore assoluto medio (MAE) e l’errore quadratico relativo (RRSE). Questo esperimento si concentra sui modelli TSF perché non è disponibile un grafico.

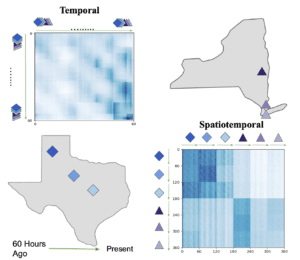
Spacetimeformer supera le linee di base e il suo vantaggio rispetto alla versione dell’attenzione temporale sembra aumentare con la lunghezza delle nostre previsioni. Il nostro obiettivo è imparare un grafo di attenzione spazio-temporale e possiamo verificare che questo è ciò che Spacetimeformer ottiene visualizzando la sua rete di attenzione. Le matrici di attenzione visualizzano l’MSA rivelando l’attenzione prestata da ciascun token all’intera sequenza; ogni riga rappresenta un token e le colonne di quella riga mostrano l’attenzione del token verso gli altri token della sequenza, incluso se stesso. La figura seguente mostra le variabili della stazione meteorologica e le matrici di attenzione di Spacetimeformer e della variante solo temporale, dove il colore blu più scuro corrisponde a una maggiore attenzione. Il meccanismo standard di Temporal apprende un modello a onda scorrevole in cui ogni token si concentra principalmente su se stesso (lungo la diagonale) e sulla fine della sequenza. Spacetimeformer appiattisce la sequenza in variabili separate, con ogni variabile che ha la sua sotto-sequenza di token (indicata da una freccia verde e dalla forma della variabile). Ne risulta una matrice di attenzione “strutturata a blocchi” in cui tutti i token di una variabile tendono a dare priorità ai tempi di un sottoinsieme di altre variabili. Possiamo interpretare questi schemi per capire le relazioni spaziali che il modello sta apprendendo. In questo caso, il modello è in grado di raggruppare correttamente le stazioni del Texas e di New York e, se si effettua uno zoom, si possono notare gli stessi schemi temporali a onda all’interno di ogni sottosequenza.

Successivamente, esaminiamo tre set di dati di riferimento per la previsione del traffico e dell’energia. AL Solar misura la produzione solare di 137 siti in Alabama, mentre i dataset Metr-LA e Pems-Bay misurano la velocità dei veicoli con oltre 200 sensori stradali rispettivamente a Los Angeles e San Francisco. Generiamo previsioni solari a 4 ore e previsioni del traffico a 1 ora. I risultati sono riportati nelle tabelle seguenti.

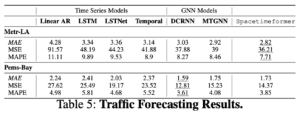
Spacetimeformer apprende un modello di previsione accurato in tutti i casi. I risultati sul traffico sono interessanti perché la complessità della rete stradale rende questi problemi un benchmark comune nella ricerca sulle reti neurali grafiche, dove la mappa può essere trasformata in un grafo e fornita al modello in anticipo. Il nostro modello ha un potere predittivo comparabile, pur apprendendo implicitamente una mappa stradale dai dati.

Se desiderate applicare questo metodo a nuovi problemi, il codice sorgente del modello e del processo di addestramento è disponibile su GitHub all’indirizzo QData/spacetimeformer. Una spiegazione più dettagliata, con ulteriori informazioni di base e lavori correlati, è disponibile nel nostro documento.

Articolo originale di Jake Grigsby
Multivariate Time Series Forecasting with Transformers | by Jake Grigsby | Towards Data Science