Simulazione Montecarlo: una guida pratica
Un metodo versatile per la stima dei parametri. Esempio di implementazione nel linguaggio di programmazione Python.
Articolo in lingua originale di Robert Kwiatkowski

La simulazione (o metodo) Monte Carlo è una tecnica numerica probabilistica utilizzata per stimare il risultato di un processo incerto (stocastico). Ciò significa che è un metodo per simulare eventi che non possono essere modellati in modo implicito. Questo è solitamente il caso di variabili casuali nei nostri processi.
In questo articolo, vi fornirò un breve background di questa tecnica, mostrerò i passi da seguire per implementarla e, alla fine, ci saranno due esempi di problemi risolti utilizzando Monte Carlo nel linguaggio di programmazione Python.
Un po’ di storia
La simulazione Monte Carlo, come molti altri metodi numerici, è stata inventata prima dell’avvento dei computer moderni – è stata sviluppata durante la seconda guerra mondiale – da due matematici: Stanisław Ulam e John von Neumann. All’epoca erano entrambi coinvolti nel progetto Manhattan e idearono questa tecnica per simulare una reazione a catena nell’uranio altamente arricchito. In poche parole, stavano simulando un’esplosione atomica.
Risolvere il problema della “diffusione di neutroni” era troppo complesso da descrivere e da risolvere in modo esplicito, soprattutto se si considera che disponevano solo di macchine IBM a schede perforate o, più tardi, di un computer chiamato ENIAC. Durante la sua degenza in ospedale, Stanisław Ulam stava ammazzando la noia giocando a carte quando gli venne una nuova idea. Dopo essere tornato al lavoro, condivise la sua idea con il collega di laboratorio John von Neumann. Lo sviluppo di un nuovo metodo risolutivo prese il nome in codice di “Monte Carlo”. Questo metodo si basava sul campionamento casuale e sulla statistica. Grazie ad esso entrambi i matematici furono in grado di accelerare il processo di calcolo, di fare previsioni incredibilmente buone e di fornire al progetto risultati utili e molto richiesti all’epoca.

Nel 1949, mentre lavorava al laboratorio Los Alamos National Laboratory, Stanisław Ulam pubblicò il primo documento non-classificato che descrive la simulazione Montecarlo.
Applicazioni contemporanee
Attualmente, a causa della facilità dell’implementazione e all’elevata potenza di calcolo disponibile, questa tecnica è ampiamente utilizzata in diversi settori. Vediamo alcuni casi d’uso documentati
Salute:
- “A random walk Monte Carlo simulation study of COVID-19-like infection spread”
- “Human health risk assessment of toxic elements in South Korean cabbage, Kimchi, using Monte Carlo simulation”
Finanza:
- “Sensitivity estimation of conditional value at risk using randomized quasi-Monte Carlo”
- “Complex system in finance: Monte Carlo evaluation of first passage time density function”
Produzione:
- “Robustness evaluation of production plans using Monte Carlo Simulation”
- “Monte Carlo Tree Search for online decision making in smart industrial production”
Trasporti:
Ingegneria/Scienza:
- Design and optimization of graphene quantum dot-based luminescent solar concentrator using Monte-Carlo simulation
- “Risk analysis of an underground gas storage facility using a physics-based system performance model and Monte Carlo simulation”
- “Nonlinear robust fault diagnosis of power plant gas turbine using Monte Carlo-based adaptive threshold approach”
Scheletro del metodo Monte Carlo
Il concetto centrale della simulazione Monte Carlo è un campionamento casuale multiplo da un insieme di distribuzioni di probabilità. Queste possono essere di qualsiasi tipo, ad esempio: normali, continue, triangolari, Beta, Gamma e così via.
Per utilizzare questa tecnica, è necessario seguire quattro fasi principali:
- Identificare tutti i componenti di input del processo e come interagiscono, ad esempio: si sommano o si sottraggono?
- Definire i parametri delle distribuzioni.
- Campionare da ciascuna delle distribuzioni e integrare i risultati in base al punto 1.
- Ripetere il processo tutte le volte che si vuole.
Durante l’esecuzione di questa simulazione, il parametro risultante (ad esempio, il costo o il rischio) convergerà verso la distribuzione normale, anche se le distribuzioni di origine possono essere diverse. Questo è l’effetto del Teorema del limite centrale ed è uno dei motivi per cui questa tecnica è diventata immensamente popolare in vari settori.
Implementazione in Python - le basi
La simulazione Monte Carlo può essere facilmente implementata utilizzando qualsiasi linguaggio di programmazione. In questo caso utilizzeremo Python.
La libreria NumPy sarà molto comoda dal momento che ha molte delle più popolari distribuzioni di probabilità implementate. Ad esempio:
- numpy.random.normal — distribuzione normale
- numpy.random.triangular — distribuzione triangolare
- numpy.random.uniform — distribuzione uniforme
- numpy.random.weibull — distribuzione Weibull
Esempio 1
Supponiamo di avere un processo costruito da 3 fasi (X1, X2, X3). Ognuna di esse ha una durata media (5, 10 e 15 minuti) che varia secondo la distribuzione normale e di cui conosciamo la varianza (1 minuto per tutte).
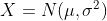

Vogliamo sapere qual è la probabilità che il processo superi i 34 minuti. Questo esempio è talmente banale che può essere risolto manualmente, come faremo in seguito per convalidare il risultato del metodo Monte Carlo.
Conosciamo tutti le singole componenti, quindi definiamo la relazione tra di esse (è additiva):
![]()
Ora possiamo iniziare a scrivere il codice. La singola componente può essere rappresentata con una breve funzione:
import numpy.random as rnd def mc_normal(mean, std_dev, samples): "Sampling from the Normal Distribution)" results = [] for _ in range(samples): results.append(rnd.normal(mean, std_dev)) return np.array(results)
Il codice della simulazione Monte Carlo mostrato di seguito utilizza questa funzione come blocco di base.
Il numero di iterazioni per questo caso d’uso è impostato a 10 000, ma è possibile modificarlo. L’ultima sezione del codice verifica la probabilità di uscire dal limite di 34 minuti (ancora una volta utilizza la tecnica del campionamento).
# configuration
s = 100000 # number of samples
upper_limit = 34 # upper limit from specification
# components
component_1 = mc_normal(5,1,s)
component_2 = mc_normal(10,1,s)
component_3 = mc_normal(15,1,s)
# relationships
total = component_1 + component_2 + component_3
# success conditions
probability = np.sum(total > upper_limit)/len(total)*100
print("Probability of exceeding the time limit: ", round(probability, 3), "%")
Dopo aver eseguito il codice seguente otteniamo la seguente risposta che può variare ogni volta che eseguiamo il codice:
Probability of exceeding the time limit: 1.035 %
Ora possiamo plottare l’istogramma del parametro stimato (il tempo). Possiamo vedere chiaramente che segue una distribuzione normale.

Verifichiamolo manualmente con dei calcoli:
![]()
![]()
Come risultato otteniamo che il tempo segue una distribuzione normale con parametri: Y = N(30, 3)
Per calcolare la probabilità dobbiamo trovare prima lo z-score:
![]()
Possiamo leggere il p-value dalla tabella dello z-score. Calcoliamo la probabilità della coda di destra come:
![]()
Come ricordate, la nostra simulazione Monte Carlo ci ha dato come risultato 1.05% che è molto vicino a questo.
Esempio 2
In questo esempio assumiamo di voler assemblare tre blocchi all’interno di un contenitore di una determinata larghezza. Le dimensioni nominali sono riportate nell’immagine sottostante. Vediamo che da progetto c’è uno spazio nominale di 0,5 mm.

Tuttavia, le dimensioni reali di questi tre blocchi e di un contenitore possono variare per motivi tecnici. A scopo dimostrativo, assumiamo che nessuna di queste variazioni segua la distribuzione normale. I tre blocchi seguiranno le distribuzioni triangolari illustrate di seguito e le dimensioni del contenitore seguiranno una distribuzione uniforme in un intervallo di +/-0,1 mm.

Ora, calcolando semplicemente i valori estremi, possiamo vedere che nello scenario peggiore i blocchi hanno 17 mm e un contenitore ha una larghezza di soli 16,4 mm, il che significa che, in questo caso, non possiamo inserirli tutti insieme.
La domanda è: qual è la probabilità di non riuscire a inserire tutti i blocchi in un contenitore?
In questo caso, le relazioni tra i blocchi appaiono come = Y = X4 – X1 – X2 – X3
Modificando il codice precedente otteniamo una funzione per campionare la distribuzione triangolare. Lo stesso possiamo farlo per ottenere la funzione di campionamento della distribuzione uniforme.
def mc_triangle(left, mode, right, samples): results = [] for _ in range(samples): results.append(rnd.triangular(left, mode, right)) return np.array(results)
Un codice di base modificato per la simulazione MC:
# configuration
s = 100000 # number of samples
limit = 0 # limit from specification
# components
component_1 = mc_triangle(3.8, 4.0, 4.4,s)
component_2 = mc_triangle(5.9, 6.0, 6.5,s)
component_3 = mc_triangle(5.8, 6.0, 6.1,s)
component_4 = mc_uniform(16.4, 16.6, s)
# relationships
total = component_4 - component_1 - component_2 - component_3
# success conditions
probability = np.sum(total < limit)/len(total)*100
print("Probability of not fitting the blocks: ", round(probability, 4), "%")
Dopo aver eseguito il codice precedente otteniamo una risposta nell’ordine di:
Probability of not fitting the blocks: 5.601 %
Dopo aver controllato la media e la deviazione standard, possiamo dire ancora di più sulla dimensione del divario atteso:
print('The mean gap width will be {}mm with a standard deviation of {}mm.'.format(round(np.mean(total), 2) ,round(np.std(total),2)))
The mean gap width will be 0.33mm with a standard deviation of 0.2mm.
Ora plottiamo l’istogramma del parametro stimato (larghezza del gap) per mostrare che segue una distribuzione normale nonostante nessuna delle distribuzioni in input era di questo tipo.

Ci si può ora chiedere come varierà il risultato all’aumentare del numero di campioni. Per verificarlo, si veda il grafico seguente che mostra la stima della larghezza del gap con un intervallo di confidenza del 95%, a seconda della dimensione del campione (da 100 a 7000 campioni):

Da questo grafico è evidente che la media del valore stimato non cambia in modo significativo, ma lo diffusione diminuisce con il numero di campioni. Ciò significa che con una nuova esecuzione della simulazione, campioni più grandi consentono di ottenere una minore diffusione dei risultati.
Tuttavia, a un certo punto l’aggiunta di più campioni non è più utile.
Sintesi
Come avete visto il metodo Monte Carlo si basa su un’idea molto semplice seppur molto potente. Dopo aver letto questo articolo spero che abbiate capito il concetto chiave del metodo, quando utilizzarlo e come implementarlo nel linguaggio di programmazione Python.
Share:


