Un’introduzione intuitiva alle reti avversarie generative (GAN)
Riscaldarsi
Supponiamo che nel vostro quartiere si stia svolgendo una festa molto bella a cui vorreste davvero andare. Ma c’è un problema. Per entrare alla festa è necessario un biglietto speciale, che è stato esaurito da tempo.
Aspettate! Questo non è un articolo sulle reti avversarie generative? Sì, lo è. Ma portate pazienza per ora, ne varrà la pena.
Ok, visto che le aspettative sono molto alte, gli organizzatori della festa hanno assunto un’agenzia di sicurezza qualificata. Il loro obiettivo primario è quello di non permettere a nessuno di imbucarsi alla festa. Per questo hanno piazzato molte guardie all’ingresso del locale per controllare l’autenticità dei biglietti di tutti.
Poiché non si hanno doti artistiche marziali, l’unico modo per passare è ingannarli con un biglietto falso molto convincente.
C’è però un grosso problema in questo piano: non avete mai visto come è fatto il biglietto.
Anche se si progetta un biglietto basato sulla propria creatività, è quasi impossibile ingannare le guardie alla prima prova. Inoltre, non potete mostrare il vostro volto finché non avrete una copia molto decente del pass della festa.
Per risolvere il problema, decidete di chiamare il vostro amico Bob a fare il lavoro per voi.
La missione di Bob è molto semplice. Cercherà di entrare alla festa con il pass falso. Se gli viene negato, tornerà da voi con consigli utili su come dovrebbe essere il biglietto.
Sulla base di questi suggerimenti, si crea una nuova versione del biglietto e la si consegna a Bob, che ci riprova. Questo processo si ripete fino a quando non si riesce a progettare una replica perfetta.
Mettendo da parte i “piccoli buchi” di questo aneddoto, è più o meno così che funzionano le reti avversarie generative (GAN).
Al giorno d’oggi, la maggior parte delle applicazioni delle GAN sono nel campo della computer vision. Alcune di queste applicazioni includono l’addestramento di classificatori semi-supervisionati e la generazione di immagini ad alta risoluzione da controparti a bassa risoluzione.
Questo articolo fornisce un’introduzione alle GAN con un approccio pratico al problema della generazione di immagini. È possibile clonare il notebook di questo post qui.
Reti avversarie generative
Le GAN sono modelli generativi ideati da Goodfellow et al. nel 2014. In una configurazione GAN, due funzioni differenziabili, rappresentate da reti neurali, sono bloccate in un gioco. I due giocatori (il generatore e il discriminatore) hanno ruoli diversi.
Il generatore cerca di produrre dati che provengono da una certa distribuzione di probabilità. In questo caso, l’utente cerca di riprodurre i biglietti della festa.
Il discriminatore agisce come un giudice. Deve decidere se l’input proviene dal generatore o dal vero set di addestramento. In questo caso, la sicurezza della festa confronta il vostro biglietto falso con il biglietto vero per trovare difetti nel vostro progetto.
Abbiamo utilizzato una rete di convoluzione a 4 strati (sia per il discriminatore che per il generatore) con normalizzazione batch. Il modello è stato addestrato per generare SVHN e immagini MNIST. In alto, i campioni dei generatori SVHN (a sinistra) e MNIST (a destra) durante l’addestramento.
In sintesi, il gioco segue con:
– Il generatore cerca di massimizzare la probabilità di far sì che il discriminatore scambi i suoi input come reali.
– E il discriminatore che guida il generatore a produrre immagini più realistiche.
In un equilibrio perfetto, il generatore catturerebbe la distribuzione generale dei dati di addestramento. Di conseguenza, il discriminatore sarebbe sempre incerto se i suoi input sono reali o meno.
Nel documento DCGAN, gli autori descrivono la combinazione di alcune tecniche di deep learning come chiave per l’addestramento delle GAN. Queste tecniche includono: (i) la rete convoluzionale completa e (ii) la normalizzazione dei lotti (BN).
La prima enfatizza le convoluzioni stridenti (invece di unire gli strati) sia per aumentare che per diminuire le dimensioni spaziali delle caratteristiche. La seconda normalizza i vettori delle caratteristiche in modo che abbiano media zero e varianza unitaria in tutti gli strati. Questo aiuta a stabilizzare l’apprendimento e a gestire i problemi di scarsa inizializzazione dei pesi.
Senza ulteriori indugi, entriamo nei dettagli dell’implementazione e parliamo di GAN man mano che procediamo. Presentiamo un’implementazione di una Deep Convolutional Generative Adversarial Network (DCGAN). La nostra implementazione utilizza Tensorflow e segue alcune pratiche descritte nel documento DCGAN.
Generatore
La rete ha 4 strati convoluzionali, tutti seguiti da BN (tranne lo strato di uscita) e attivazioni di unità lineari rettificate (ReLU).
Prende in ingresso un vettore casuale z (estratto da una distribuzione normale). Dopo aver rimodellato z in modo che abbia una forma 4D, lo diamo in pasto al generatore che avvia una serie di strati di upsampling.
Ogni livello di upsampling rappresenta un’operazione di convoluzione di trasposizione con passo 2. Le convoluzioni di trasposizione sono simili alle convoluzioni regolari.
In genere, le convoluzioni regolari passano da strati ampi e poco profondi a strati più stretti e profondi. Le convoluzioni di trasposizione vanno nella direzione opposta. Vanno da strati profondi e stretti a strati più larghi e meno profondi.
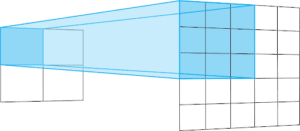
Lo stride di un’operazione di convoluzione di trasposizione definisce la dimensione del livello di uscita. Con un padding “uguale” e uno stride di 2, le caratteristiche di uscita avranno una dimensione doppia rispetto al livello di ingresso.
Questo accade perché, ogni volta che si sposta un pixel nel livello di ingresso, si sposta il kernel di convoluzione di due pixel nel livello di uscita. In altre parole, ogni pixel dell’immagine di ingresso viene utilizzato per disegnare un quadrato nell’immagine di uscita.
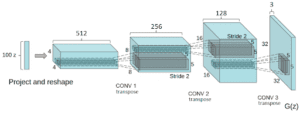
In breve, il generatore inizia con questo vettore di ingresso molto profondo ma stretto. Dopo ogni convoluzione di trasposizione, z diventa più ampio e meno profondo. Tutte le convoluzioni di trasposizione utilizzano un kernel di dimensioni 5×5 con profondità da 512 a 3, che rappresenta un’immagine a colori RGB.
def transpose_conv2d(x, output_space):
return tf.layers.conv2d_transpose(x, output_space,
kernel_size=5, strides=2, padding=’same’,
kernel_initializer=tf.random_normal_initializer(mean=0.0,
stddev=0.02))
Lo strato finale produce un tensore 32x32x3 – schiacciato tra i valori di -1 e 1 attraverso la funzione di tangente iperbolica (tanh).
La forma finale dell’output è definita dalla dimensione delle immagini di addestramento. In questo caso, se l’addestramento avviene per SVHN, il generatore produce 32x32x3 immagini. Tuttavia, se si addestra per MNIST, genererebbe un’immagine in scala di grigi 28×28.
Infine, si noti che prima di dare in pasto al generatore il vettore di ingresso z, è necessario scalarlo nell’intervallo da -1 a 1. Questo per seguire la scelta di utilizzare la funzione tanh.
def generator(z, output_dim, reuse=False, alpha=0.2, training=True):
“””
Defines the generator network
:param z: input random vector z
:param output_dim: output dimension of the network
:param reuse: Indicates whether or not the existing model variables should be used or recreated
:param alpha: scalar for lrelu activation function
:param training: Boolean for controlling the batch normalization statistics
:return: model’s output
“””
with tf.variable_scope(‘generator’, reuse=reuse):
fc1 = dense(z, 4*4*512)
# Reshape it to start the convolutional stack
fc1 = tf.reshape(fc1, (–1, 4, 4, 512))
fc1 = batch_norm(fc1, training=training)
fc1 = tf.nn.relu(fc1)
t_conv1 = transpose_conv2d(fc1, 256)
t_conv1 = batch_norm(t_conv1, training=training)
t_conv1 = tf.nn.relu(t_conv1)
t_conv2 = transpose_conv2d(t_conv1, 128)
t_conv2 = batch_norm(t_conv2, training=training)
t_conv2 = tf.nn.relu(t_conv2)
logits = transpose_conv2d(t_conv2, output_dim)
out = tf.tanh(logits)
return out
Discriminatore
Anche il discriminatore è una CNN a 4 strati con attivazioni BN (tranne lo strato di ingresso) e ReLU leaky. Molte funzioni di attivazione funzionano bene con questa architettura GAN di base. Tuttavia, le ReLU leaky sono molto popolari perché aiutano i gradienti a scorrere più facilmente attraverso l’architettura.
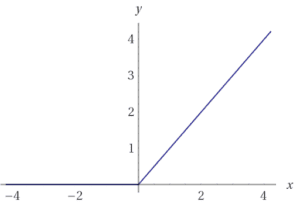
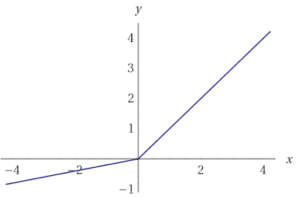
Una normale funzione ReLU funziona troncando i valori negativi a 0. Questo ha l’effetto di bloccare il flusso dei gradienti attraverso la rete. Invece di azzerare la funzione, le ReLU leaky permettono il passaggio di un piccolo valore negativo. In altre parole, la funzione calcola il valore maggiore tra le caratteristiche e un piccolo fattore.
def lrelu(x, alpha=0,2):
# funzione di attivazione non lineare
restituisce tf.maximum(alpha * x, x)
Le Leaky ReLU rappresentano un tentativo di risolvere il problema delle ReLU morenti. Questa situazione si verifica quando i neuroni si bloccano in uno stato in cui le unità ReLU producono sempre 0 per tutti gli ingressi. In questi casi, i gradienti sono completamente bloccati per tornare a fluire attraverso la rete.
Questo è particolarmente importante per le GAN, poiché l’unico modo che il generatore ha per apprendere è ricevere i gradienti dal discriminatore.
Il discriminatore inizia con la ricezione di un tensore di immagini 32x32x3. Diversamente dal generatore, il discriminatore esegue una serie di convoluzioni a 2 canali. Ciascuna di esse riduce le dimensioni spaziali del vettore di caratteristiche della metà della sua dimensione, raddoppiando anche il numero di filtri appresi.
Infine, il discriminatore deve produrre delle probabilità. A tale scopo, utilizziamo la funzione di attivazione Logistic Sigmoid sui logit finali.def discriminator(x, reuse=False, alpha=0.2, training=True):
“””
Defines the discriminator network
:param x: input for network
:param reuse: Indicates whether or not the existing model variables should be used or recreated
:param alpha: scalar for lrelu activation function
:param training: Boolean for controlling the batch normalization statistics
:return: A tuple of (sigmoid probabilities, logits)
“””
with tf.variable_scope(‘discriminator’, reuse=reuse):
# Input layer is 32x32x?
conv1 = conv2d(x, 64)
conv1 = lrelu(conv1, alpha)
conv2 = conv2d(conv1, 128)
conv2 = batch_norm(conv2, training=training)
conv2 = lrelu(conv2, alpha)
conv3 = conv2d(conv2, 256)
conv3 = batch_norm(conv3, training=training)
conv3 = lrelu(conv3, alpha)
# Flatten it
flat = tf.reshape(conv3, (–1, 4*4*256))
logits = dense(flat, 1)
out = tf.sigmoid(logits)
return out, logits
Si noti che in questa struttura il discriminatore si comporta come un normale classificatore binario. Per metà del tempo riceve immagini dall’insieme di allenamento e per l’altra metà dal generatore.
Tornando alla nostra avventura, per riprodurre il biglietto della festa, l’unica fonte di informazione era il feedback del nostro amico Bob. In altre parole, la qualità del feedback che Bob vi forniva a ogni prova era essenziale per portare a termine il lavoro.
Allo stesso modo, ogni volta che il discriminatore nota una differenza tra l’immagine vera e quella falsa, invia un segnale al generatore. Questo segnale è il gradiente che scorre all’indietro dal discriminatore al generatore. Ricevendolo, il generatore è in grado di regolare i suoi parametri per avvicinarsi alla vera distribuzione dei dati.
Ecco quanto è importante il discriminatore. Infatti, il generatore sarà tanto bravo a produrre dati quanto il discriminatore a distinguerli.
Perdite
Descriviamo ora la parte più complicata di questa architettura: le perdite. Innanzitutto, sappiamo che il discriminatore riceve immagini sia dal set di addestramento sia dal generatore.
Vogliamo che il discriminatore sia in grado di distinguere tra immagini vere e false. Ogni volta che facciamo passare un mini-batch attraverso il discriminatore, otteniamo dei logit. Questi sono i valori non scalati del modello.
Tuttavia, possiamo dividere i mini-batch che il discriminatore riceve in due tipi. Il primo, composto solo da immagini reali provenienti dall’insieme di allenamento e il secondo, con solo immagini false, quelle create dal generatore.
def model_loss(input_real, input_z, output_dim, alpha=0.2, smooth=0.1):
“””
Get the loss for the discriminator and generator
:param input_real: Images from the real dataset
:param input_z: random vector z
:param out_channel_dim: The number of channels in the output image
:param smooth: label smothing scalar
:return: A tuple of (discriminator loss, generator loss)
“””
g_model = generator(input_z, output_dim, alpha=alpha)
d_model_real, d_logits_real = discriminator(input_real, alpha=alpha)
d_model_fake, d_logits_fake = discriminator(g_model, reuse=True, alpha=alpha)
# for the real images, we want them to be classified as positives,
# so we want their labels to be all ones.
# notice here we use label smoothing for helping the discriminator to generalize better.
# Label smoothing works by avoiding the classifier to make extreme predictions when extrapolating.
d_loss_real = tf.reduce_mean(
tf.nn.sigmoid_cross_entropy_with_logits(logits=d_logits_real, labels=tf.ones_like(d_logits_real) * (1 – smooth)))
# for the fake images produced by the generator, we want the discriminator to clissify them as false images,
# so we set their labels to be all zeros.
d_loss_fake = tf.reduce_mean(
tf.nn.sigmoid_cross_entropy_with_logits(logits=d_logits_fake, labels=tf.zeros_like(d_model_fake)))
# since the generator wants the discriminator to output 1s for its images, it uses the discriminator logits for the
# fake images and assign labels of 1s to them.
g_loss = tf.reduce_mean(
tf.nn.sigmoid_cross_entropy_with_logits(logits=d_logits_fake, labels=tf.ones_like(d_model_fake)))
d_loss = d_loss_real + d_loss_fake
return d_loss, g_loss
Poiché entrambe le reti si addestrano contemporaneamente, le GAN necessitano anche di due ottimizzatori. Ciascuno di essi minimizza rispettivamente le funzioni di perdita del discriminatore e del generatore.
Vogliamo che il discriminatore produca probabilità vicine a 1 per le immagini reali e vicine a 0 per le immagini false. Per fare ciò, il discriminatore ha bisogno di due perdite. Pertanto, la perdita totale del discriminatore è la somma di queste due perdite parziali. Una per massimizzare le probabilità delle immagini reali e un’altra per minimizzare la probabilità delle immagini false.

All’inizio dell’addestramento si verificano due situazioni interessanti. In primo luogo, il generatore non sa come creare immagini che assomiglino a quelle dell’insieme di allenamento. In secondo luogo, il discriminatore non sa come classificare le immagini ricevute come reali o false.
Di conseguenza, il discriminatore riceve due tipi di lotti ben distinti. Uno, composto da immagini vere provenienti dal set di addestramento e un altro contenente segnali molto rumorosi. Con il progredire dell’addestramento, il generatore inizia a produrre immagini più simili a quelle del set di addestramento. Questo accade perché il generatore si allena ad apprendere la distribuzione dei dati che compongono le immagini del set di addestramento.
Allo stesso tempo, il discriminatore inizia a diventare molto bravo a classificare i campioni come reali o falsi. Di conseguenza, i due tipi di mini-batch iniziano ad assomigliare, nella struttura, l’uno all’altro. Ciò rende il discriminatore incapace di identificare le immagini come vere o false.
Per le perdite, utilizziamo l’entropia incrociata vaniglia con Adam come buona scelta per l’ottimizzatore.

Conclusione
Le GAN sono uno dei temi più caldi dell’apprendimento automatico. Questi modelli hanno il potenziale di sbloccare metodi di apprendimento non supervisionato che potrebbero espandere il ML verso nuovi orizzonti.
Fin dalla sua creazione, la ricerca ha sviluppato molte tecniche per l’addestramento delle GAN. In Improved Techniques for Training GANs, gli autori descrivono le tecniche più avanzate sia per la generazione di immagini che per l’apprendimento semi-supervisionato.
Se siete curiosi di approfondire questi argomenti, vi consiglio di leggere Generative Models.
Share:


