Panoramica di ResNet e delle sue varianti
Dopo la celebre vittoria di AlexNet [1] al concorso di classificazione LSVRC2012, la rete profonda Residual Network [2] è stata probabilmente il lavoro più innovativo degli ultimi anni nella comunità della computer vision/deep learning. ResNet consente di addestrare fino a centinaia o addirittura migliaia di strati, ottenendo comunque prestazioni convincenti.
Sfruttando la sua potente capacità di rappresentazione, sono state incrementate le prestazioni di molte applicazioni di computer vision diverse dalla classificazione delle immagini, come il rilevamento degli oggetti e il riconoscimento dei volti.
Da quando ResNet ha fatto parlare di sé nel 2015, molti ricercatori si sono addentrati nei segreti del suo successo e sono stati apportati molti miglioramenti all’architettura. Questo articolo è diviso in due parti: nella prima parte fornirò un po’ di nozioni di base per coloro che non hanno familiarità con ResNet, nella seconda passerò in rassegna alcuni dei documenti che ho letto di recente riguardanti diverse varianti e interpretazioni dell’architettura ResNet.
Rivisitazione di ResNet
Secondo il teorema dell’approssimazione universale, data una capacità sufficiente, sappiamo che una rete feedforward con un singolo strato è sufficiente per rappresentare qualsiasi funzione. Tuttavia, lo strato può essere massiccio e la rete è incline ad adattarsi eccessivamente ai dati. Pertanto, nella comunità dei ricercatori è diffusa l’idea che l’architettura della rete debba essere più profonda.
A partire da AlexNet, l’architettura CNN allo stato dell’arte è sempre più profonda. Mentre AlexNet aveva solo 5 strati convoluzionali, la rete VGG [3] e GoogleNet (nome in codice Inception_v1) [4] avevano rispettivamente 19 e 22 strati.
Tuttavia, l’aumento della profondità della rete non si ottiene semplicemente sovrapponendo gli strati. Le reti profonde sono difficili da addestrare a causa del noto problema del gradiente che svanisce: quando il gradiente viene retropropagato agli strati precedenti, la moltiplicazione ripetuta può rendere il gradiente infinitamente piccolo. Di conseguenza, man mano che la rete si approfondisce, le sue prestazioni si saturano o addirittura iniziano a degradarsi rapidamente.
Prima di ResNet, c’erano stati diversi modi per affrontare il problema del gradiente che svanisce, ad esempio [4] aggiunge una perdita ausiliaria in uno strato intermedio come supervisione aggiuntiva, ma nessuno sembrava affrontare davvero il problema una volta per tutte.
L’idea centrale di ResNet è l’introduzione di una cosiddetta “connessione di scorciatoia identitaria” che salta uno o più strati, come mostrato nella figura seguente:
Gli autori di [2] sostengono che l’impilamento degli strati non dovrebbe degradare le prestazioni della rete, perché potremmo semplicemente impilare le mappature di identità (strato che non fa nulla) sulla rete attuale e l’architettura risultante avrebbe le stesse prestazioni. Ciò indica che il modello più profondo non dovrebbe produrre un errore di addestramento superiore alle sue controparti meno profonde. Si ipotizza che far sì che gli strati sovrapposti si adattino a una mappatura residua sia più facile che farli adattare direttamente alla mappatura sottostante desiderata. E il blocco residuo di cui sopra consente esplicitamente di fare proprio questo.
In effetti, ResNet non è stato il primo a fare uso delle connessioni di scorciatoia: Highway Network [5] ha introdotto le connessioni di scorciatoia gated. Questi cancelli parametrizzati controllano la quantità di informazioni che possono fluire attraverso la scorciatoia. Un’idea simile si ritrova nella cella della memoria corta a lungo termine (LSTM) [6], in cui è presente una porta di dimenticanza parametrizzata che controlla la quantità di informazioni che passano al passo temporale successivo. Pertanto, ResNet può essere considerata un caso speciale di Highway Network.
Tuttavia, gli esperimenti dimostrano che Highway Network non ha prestazioni migliori di ResNet, il che è piuttosto strano perché lo spazio delle soluzioni di Highway Network contiene ResNet, quindi dovrebbe avere prestazioni almeno pari a quelle di ResNet. Ciò suggerisce che è più importante mantenere libere queste “autostrade del gradiente” piuttosto che puntare su uno spazio di soluzione più ampio.
Seguendo questa intuizione, gli autori di [2] hanno perfezionato il blocco residuo e proposto una variante di pre-attivazione del blocco residuo [7], in cui i gradienti possono fluire attraverso le connessioni di scorciatoia verso qualsiasi altro strato precedente senza ostacoli. In effetti, utilizzando il blocco residuo originale di [2], l’addestramento di una ResNet a 1202 strati ha dato luogo a prestazioni peggiori rispetto alla sua controparte a 110 strati.
Gli autori di [7] hanno dimostrato con degli esperimenti che è possibile addestrare una ResNet profonda a 1001 strati per superare le sue controparti meno profonde. Grazie ai suoi risultati convincenti, ResNet è diventata rapidamente una delle architetture più popolari in vari compiti di computer vision.
Varianti e interpretazioni recenti di ResNet
Man mano che ResNet guadagna sempre più popolarità nella comunità dei ricercatori, la sua architettura viene studiata in modo approfondito. In questa sezione, presenterò innanzitutto diverse nuove architetture basate su ResNet, quindi presenterò un articolo che fornisce un’interpretazione del trattamento di ResNet come un insieme di molte reti più piccole.
ResNeXt
Xie et al. [8] hanno proposto una variante di ResNet, il cui nome in codice è ResNeXt, con la seguente struttura:
Potrebbe sembrarvi familiare, perché è molto simile al modulo Inception di [4]: entrambi seguono il paradigma split-transform-merge, solo che in questa variante gli output dei diversi percorsi vengono uniti sommandoli, mentre in [4] vengono concatenati in profondità. Un’altra differenza è che in [4] ogni percorso è diverso (convoluzione 1×1, 3×3 e 5×5) dall’altro, mentre in questa architettura tutti i percorsi condividono la stessa topologia.
Gli autori hanno introdotto un iperparametro chiamato cardinalità – il numero di percorsi indipendenti – per fornire un nuovo modo di regolare la capacità del modello. Gli esperimenti dimostrano che l’accuratezza può essere guadagnata in modo più efficiente aumentando la cardinalità piuttosto che andando più in profondità o più in larghezza. Gli autori affermano che, rispetto a Inception, questa nuova architettura è più facile da adattare a nuovi set di dati/compiti, poiché ha un paradigma semplice e un solo iperparametro da regolare, mentre Inception ha molti iperparametri (come la dimensione del kernel dello strato convoluzionale di ogni percorso) da regolare.
Questo nuovo blocco di costruzione ha tre forme equivalenti:
In pratica, la “divisione-trasformazione-fusione” viene solitamente eseguita da uno strato convoluzionale raggruppato in modo puntuale, che divide il suo ingresso in gruppi di mappe di caratteristiche ed esegue la convoluzione normale rispettivamente, le loro uscite vengono concatenate in profondità e poi alimentate a uno strato convoluzionale 1×1.
CNN densamente connessa
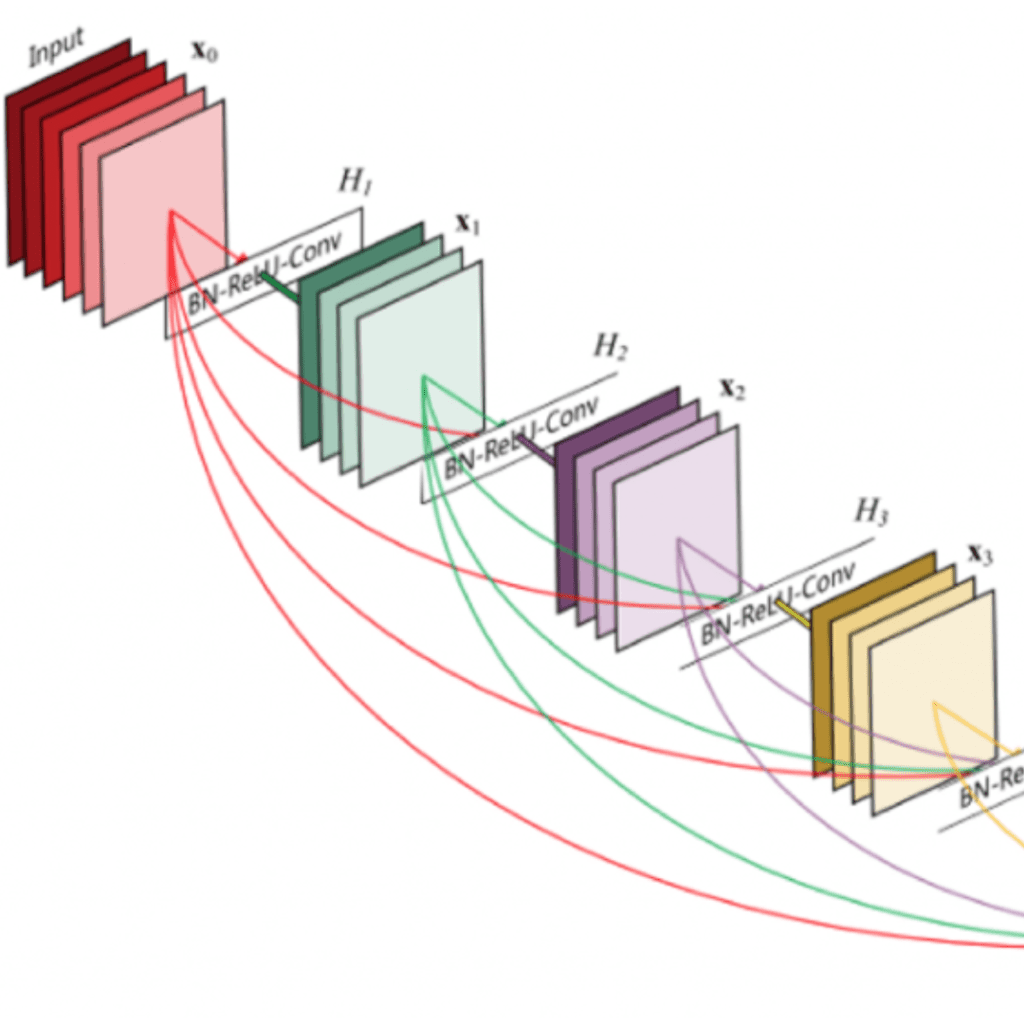
Huang et al. [9] hanno proposto una nuova architettura, chiamata DenseNet, che sfrutta ulteriormente gli effetti delle connessioni a scorciatoia, collegando tutti gli strati direttamente tra loro. In questa nuova architettura, l’ingresso di ogni strato è costituito dalle mappe di caratteristiche di tutti gli strati precedenti e l’uscita viene passata a ogni strato successivo. Le mappe di caratteristiche sono aggregate con una concatenazione di profondità.
Oltre a risolvere il problema dei gradienti che svaniscono, gli autori di [8] sostengono che questa architettura incoraggia anche il riutilizzo delle caratteristiche, rendendo la rete altamente efficiente dal punto di vista dei parametri. Una semplice interpretazione di ciò è che, in [2][7], l’output della mappatura dell’identità veniva aggiunto al blocco successivo, il che potrebbe ostacolare il flusso di informazioni se le mappe di caratteristiche di due strati hanno distribuzioni molto diverse. Pertanto, la concatenazione delle mappe di caratteristiche può preservarle tutte e aumentare la varianza degli output, favorendo il riutilizzo delle caratteristiche.
Seguendo questo paradigma, sappiamo che il livello l_esimo avrà k * (l-1) + k_0 mappe di caratteristiche in ingresso, dove k_0 è il numero di canali dell’immagine in ingresso. Gli autori hanno utilizzato un iperparametro chiamato tasso di crescita (k) per evitare che la rete si allarghi troppo; hanno inoltre utilizzato uno strato convoluzionale 1×1 a collo di bottiglia per ridurre il numero di mappe di caratteristiche prima della costosa convoluzione 3×3.
Rete profonda con profondità stocastica
Sebbene ResNet si sia dimostrata potente in molte applicazioni, uno dei principali svantaggi è che la rete profonda richiede di solito settimane per l’addestramento, il che la rende praticamente impraticabile nelle applicazioni reali. Per affrontare questo problema, Huang et al. [10] hanno introdotto un metodo controintuitivo che prevede l’abbandono casuale degli strati durante l’addestramento e l’utilizzo dell’intera rete durante i test.
Gli autori hanno utilizzato il blocco residuo come elemento costitutivo della rete; pertanto, durante l’addestramento, quando un particolare blocco residuo è abilitato, il suo input passa sia attraverso la scorciatoia di identità che attraverso gli strati di peso, altrimenti l’input passa solo attraverso la scorciatoia di identità. Durante l’addestramento, ogni strato ha una “probabilità di sopravvivenza” e viene abbandonato in modo casuale. In fase di test, tutti i blocchi vengono mantenuti attivi e ricalibrati in base alla loro probabilità di sopravvivenza durante l’addestramento.
Formalmente, lasciamo che H_l sia l’uscita dell’l_esimo blocco residuo, f_l sia la mappatura definita dalla mappatura ponderata dell’l_esimo blocco, b_l sia una variabile casuale Bernoulli che sia solo 1 o 0 (indicando se un blocco è attivo), durante l’addestramento:
Quando b_l = 1, questo blocco diventa un blocco residuo normale, mentre quando b_l = 0, la formula precedente diventa:
Poiché sappiamo che H_(l-1) è l’uscita di una ReLU, che è già non negativa, l’equazione precedente si riduce a uno strato di identità che passa solo l’input allo strato successivo:
Sia p_l la probabilità di sopravvivenza dello strato l durante l’addestramento, durante il test si ha:
Gli autori hanno applicato una regola di decadimento lineare alla probabilità di sopravvivenza di ogni strato, sostenendo che, poiché gli strati precedenti estraggono caratteristiche di basso livello che saranno utilizzate da quelli successivi, non dovrebbero essere abbandonati troppo frequentemente; la regola risultante diventa quindi:
Dove L indica il numero totale di blocchi, quindi p_L è la probabilità di sopravvivenza dell’ultimo blocco residuo ed è fissata a 0,5 per tutti gli esperimenti. Si noti inoltre che in questa impostazione l’ingresso è trattato come il primo strato (l = 0) e quindi non viene mai abbandonato. Il quadro generale dell’addestramento stocastico della profondità è illustrato nella figura seguente.
Durante l'addestramento, ogni strato ha una probabilità di essere disattivato.
In modo simile a Dropout [11], l’addestramento di una rete profonda con profondità stocastica può essere visto come l’addestramento di un insieme di molte Reti di Risonanza più piccole. La differenza è che questo metodo elimina casualmente un intero strato, mentre Dropout elimina solo una parte delle unità nascoste di uno strato durante l’addestramento.
Gli esperimenti dimostrano che l’addestramento di una ResNet a 110 strati con profondità stocastica produce prestazioni migliori rispetto all’addestramento di una ResNet a 110 strati a profondità costante, riducendo al contempo drasticamente il tempo di addestramento. Ciò suggerisce che alcuni strati (percorsi) di ResNet potrebbero essere ridondanti.
ResNet come insieme di reti più piccole
[10] ha proposto un metodo controintuitivo per addestrare una rete molto profonda, eliminando casualmente i suoi strati durante l’addestramento e utilizzando la rete completa in fase di test. Veit et al. [14] hanno scoperto una cosa ancora più controintuitiva: è possibile eliminare alcuni strati di una rete ResNet addestrata e ottenere comunque prestazioni comparabili. Questo rende l’architettura di ResNet ancora più interessante, poiché [14] ha anche eliminato alcuni strati di una rete VGG, degradandone drasticamente le prestazioni.
[14] fornisce prima di tutto una visione srotolata di ResNet per rendere le cose più chiare. Dopo aver srotolato l’architettura della rete, è chiaro che un’architettura ResNet con i blocchi residui ha 2 ** i percorsi diversi (perché ogni blocco residuo fornisce due percorsi indipendenti).
Alla luce di questa constatazione, è chiaro che la rimozione di un paio di strati in un’architettura ResNet non compromette troppo le sue prestazioni: l’architettura ha molti percorsi efficaci indipendenti e la maggior parte di essi rimane intatta dopo la rimozione di un paio di strati. Al contrario, la rete VGG ha un solo percorso effettivo, quindi la rimozione di un singolo strato compromette questo unico percorso. Come dimostrato dagli esperimenti approfonditi in [14].
Gli autori hanno anche condotto esperimenti per dimostrare che la collezione di percorsi in ResNet ha un comportamento simile a un ensemble. Lo fanno eliminando un numero diverso di strati al momento del test e verificando se le prestazioni della rete sono correlate al numero di strati eliminati. I risultati suggeriscono che la rete si comporta effettivamente come un ensemble, come mostrato nella figura seguente:
l’errore aumenta dolcemente all’aumentare del numero di strati eliminati
Infine, gli autori hanno esaminato le caratteristiche dei percorsi in ResNet:
È evidente che la distribuzione di tutte le possibili lunghezze dei percorsi segue una distribuzione binomiale, come mostrato in (a) della figura seguente. La maggior parte dei percorsi attraversa da 19 a 35 blocchi residui.
Per studiare la relazione tra la lunghezza del percorso e l’entità dei gradienti che lo attraversano. Per ottenere l’entità dei gradienti nel percorso di lunghezza k, gli autori hanno prima alimentato la rete con un lotto di dati e hanno campionato casualmente k blocchi residui. Durante la propagazione all’indietro dei gradienti, questi si propagano attraverso lo strato dei pesi solo per i blocchi residui campionati. (b) mostra che l’entità dei gradienti diminuisce rapidamente quando il percorso diventa più lungo.
Possiamo ora moltiplicare la frequenza di ciascuna lunghezza di percorso con la sua grandezza attesa di gradienti per avere un’idea di quanto i percorsi di ciascuna lunghezza contribuiscano all’addestramento, come in (c). Sorprendentemente, la maggior parte dei contributi proviene dai percorsi di lunghezza compresa tra 9 e 18, ma essi costituiscono solo una piccola parte dei percorsi totali, come in (a). Si tratta di un risultato molto interessante, in quanto suggerisce che ResNet non ha risolto il problema della scomparsa dei gradienti per i percorsi molto lunghi, e che in realtà ResNet consente di addestrare reti molto profonde accorciando i percorsi effettivi.
Conclusione
In questo articolo ho rivisitato l’interessante architettura di ResNet, spiegando brevemente le intuizioni alla base del suo recente successo. In seguito, ho presentato diversi articoli che propongono interessanti varianti di ResNet o ne forniscono un’interpretazione perspicace. Spero che ciò contribuisca a rafforzare la vostra comprensione di questo lavoro innovativo.
Tutte le figure presenti in questo articolo sono state tratte dai documenti originali riportati nei riferimenti.
Se siete interessati ad approfondire anche le altre CNN più performanti, così come altre applicazioni delle reti convoluzionali (es. Object Detection), iscrivetevi al corso di Computer Vision Hands-On.
Articolo originale di Vincent Feng
An Overview of ResNet and its Variants | by Vincent Feng | Towards Data Science
Share: